Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 10. 2012 16:34
Úprava výrazu s komplex. čísly
Ahoj,
mám na první pohled jednoduchý zlomek 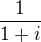 a ten se nějakou (zřejmě jednoduchou úpravou, dělaná bez mezikroku) dá přepsat na
a ten se nějakou (zřejmě jednoduchou úpravou, dělaná bez mezikroku) dá přepsat na 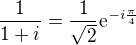 .
.
Může mi někdo prosím vysvětlit tuto úpravu? Nemůžu se k tomu dopracovat. Děkuji
pozn.:  je komplexní jednotka
je komplexní jednotka
Offline
- (téma jako vyřešené označil(a) darkmagic)
#2 22. 10. 2012 16:58 — Editoval Andrejka3 (22. 10. 2012 16:58)
Re: Úprava výrazu s komplex. čísly
↑ darkmagic:
Ahoj,
pro každé nenulové komplexní číslo  platí
platí
Je-li 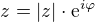 , pak jeho inverze je
, pak jeho inverze je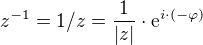 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
