Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Zajímavé úlohy z algebry
- » determinant obecné matice (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 11. 2012 20:32
determinant obecné matice
Zdravím.
Je dána matice řádu nxn:
a1 x x ... x
x a2 x ... x
x x a3 ... x
. . . .
. . . .
x x x an
úkolem je spočítat determinant. Myslíte že se dá odvodit nějaké řešení pro n? Díky
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
- (téma jako vyřešené označil(a) Honza90)
#2 09. 11. 2012 21:01
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: determinant obecné matice
↑ Honza90:
Ahoj, ta "x" jsou libovolné prvky (v každém poli obecně různé) a nebo se jedná ve všech polích o jeden stále stejný prvek (x)?
"Máte úhel beta." "No to nemám."
Offline
#3 09. 11. 2012 21:05
Re: determinant obecné matice
↑ check_drummer:
x je všude jeden a ten samý prvek
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#4 09. 11. 2012 21:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
↑ Honza90:
Ahoj,
myslím, že ano.
Postupoval jsem tak, že jsem poslední sloupec odečetl od všech zbylých. Potom jsem udělal Laplaceův rozvoj podle prvního řádku. Dostal jsem dva členy. V jednom se objeví stejný determinant s prvky 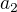 až
až  . V druhém členu provedeme rozvoj podle prvního sloupce. Takhle dostaneme předpis pro determinant matice nxn pomocí determinantu matice (n-1)x(n-1). Spočítal jsem si prvních pár determinantů, odhadl obecný vzorec a ten matematickou indukcí dokázal. Vyšlo mi
. V druhém členu provedeme rozvoj podle prvního sloupce. Takhle dostaneme předpis pro determinant matice nxn pomocí determinantu matice (n-1)x(n-1). Spočítal jsem si prvních pár determinantů, odhadl obecný vzorec a ten matematickou indukcí dokázal. Vyšlo mi
Offline
#5 09. 11. 2012 21:50
Re: determinant obecné matice
↑ Pavel Brožek:
No moc přesvědčen nejsem. Po odečtení posledního sloupce od ostatních dostanu v posledním řádku členy typu 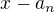 ale ty ve tvém vzorci chybí.
ale ty ve tvém vzorci chybí.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#6 09. 11. 2012 22:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
↑ Honza90:
No když si po tom odečtení posledního sloupce uděláš rozvoj podle posledního řádku, tak uvidíš, že dostaneš 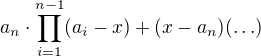 , kde ty tři tečky už nezávisí na
, kde ty tři tečky už nezávisí na  . Mně to teda přijde dost podobné tomu mému řešení. Snad tě to už přesvědčilo dostatečně, aby sis ten postup prošel, opravdu se mi tu nechce vypisovat se s těmi maticemi, na papíře je to jednodušší. :-)
. Mně to teda přijde dost podobné tomu mému řešení. Snad tě to už přesvědčilo dostatečně, aby sis ten postup prošel, opravdu se mi tu nechce vypisovat se s těmi maticemi, na papíře je to jednodušší. :-)
A ani bych neřekl, že v mém vzorci chybí. V prvním členu je ten člen vždy, v tom druhém je tam pro  .
.
Offline
#7 09. 11. 2012 22:54 — Editoval Honza90 (09. 11. 2012 22:59)
Re: determinant obecné matice
↑ Pavel Brožek:
Já na to chtěl jít jen pomocí permutací a vyhnout se úplně Laplaceovi, ale to se nepodařilo. Takhle je to asi jediný způsob, i když do toho teď úplně nevidím. Např. jak to bude se znaménky?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 09. 11. 2012 23:04
Re: determinant obecné matice
Poznamka
Ja by som skor od prveho stlpca odpocital druhy
od druheho treti
atd a nakoniec by som rozvynul podla posledneho stlpca.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 09. 11. 2012 23:20 — Editoval vanok (10. 11. 2012 03:39)
Re: determinant obecné matice
Vysledok:
Zda sa mi, ze hladany determinant je
Édit: tento vysledok je SPATNY
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 10. 11. 2012 00:33 — Editoval Pavel Brožek (10. 11. 2012 00:36)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
↑ vanok:, ↑ Honza90:
Koukám na to jak blázen, že se shodnete na výsledku, který mi připadá na první pohled nesmyslný. Vždyť determinant je evidentně polynom v x.  rozhodně není polynom v x. Asi se vyspím a podívám se na to ráno, třeba mi dojde něco, co mi teď absolutně uniká…
rozhodně není polynom v x. Asi se vyspím a podívám se na to ráno, třeba mi dojde něco, co mi teď absolutně uniká…
Vždyť ani pro jednoduchý případ x=0 to nedá správný výsledek (ani když se to vezme v limitě).
Offline
#12 10. 11. 2012 00:54
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
Když se na to ještě dívám, tak ten můj výsledek se dá přepsat (pokud 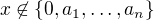 ) jako
) jako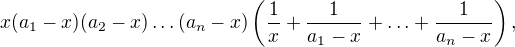
to už se značně podobá vašemu výsledku, ale přesto se to neshoduje. Asi se zítra bude muset někdo z nás rozepsat se svým řešením… :-)
Offline
#13 10. 11. 2012 03:00
Re: determinant obecné matice
Ahoj ↑ Pavel Brožek:,
Tvoj vysledok je spravny.
To som asi uz na poly spal.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 10. 11. 2012 03:15 — Editoval check_drummer (10. 11. 2012 20:21)
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: determinant obecné matice
Ahoj, také přispěju svou troškou do diskuse (rovněž neskrývám text):
1) Odečtu od n-tého řádku řádek (n-1)-ní, od (n-1)-ního (n-2)-hý, .. od j-tého (j-1)-ní, od 2-hého 1-ní.
Takto získám v prvním řádku a1,x,x..,x), na hlavní diagonále prvky a1,a2-x,a3-x,..,an-x a na vedlejší diagonále (pod hlavní diagonálou) prvky x-a1,x-a2,..,x-an. Všude jinde budou 0.
2) Podle definice spočtu determinant.
a) Je-li v členu determinantu prvek a1 (1. řádek, 1. sloupec), musí již tento člen obsahovat všechny prvky hlavní diagonály, tj. je tvaru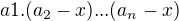 (tomuto členu odpovídá sudá permutace, tj. koeficient u členu je 1)
(tomuto členu odpovídá sudá permutace, tj. koeficient u členu je 1)
b) Je-li v členu determinantu prvek x-a1 (2. řádek, 1. sloupec), pak, jak se snadno rozmyslí, bude tento člen tvaru  . Počet transpozic je roven j-1 (do počtu traspozic přispívá jen vztah prvku x k předešlým prvkům - x je v prvním řádku), tedy koeficient tohoto členu je (-1)^{j-1}. Jak si snadno rozmyslíme, uvedený člen lze tedy upravit na tvar
. Počet transpozic je roven j-1 (do počtu traspozic přispívá jen vztah prvku x k předešlým prvkům - x je v prvním řádku), tedy koeficient tohoto členu je (-1)^{j-1}. Jak si snadno rozmyslíme, uvedený člen lze tedy upravit na tvar  . Každému j=2,...,n odpovídá jeden člen determinantu a více členů determinant nemá.
. Každému j=2,...,n odpovídá jeden člen determinantu a více členů determinant nemá.
Nyní by stačilo členy sečíst a záskáme hodnotu determinantu. Použijeme však ještě úpravu, kdy budeme předpokládat, že 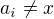 (Edit: smazána poznámka o hodnotě determinantu), položíme
(Edit: smazána poznámka o hodnotě determinantu), položíme . Pak lze výše uvedené členy upravit na:
. Pak lze výše uvedené členy upravit na:
ad 1) 
ad 2) 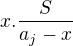
a tedy sečtením získáme hodnotu determinantu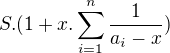 .
.
(Což je jak koukám de facto výsledek, který má i Pavel.)
"Máte úhel beta." "No to nemám."
Offline
#15 10. 11. 2012 03:18
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: determinant obecné matice
Ještě mě napadlo, zda by nebylo možné najít pro zadanou matici A vhodnou matici B takovou, že pro A.B=C bychom uměli detC i detB spočítat, pak bychom tedy znali i detA.
"Máte úhel beta." "No to nemám."
Offline
#16 10. 11. 2012 03:59 — Editoval vanok (11. 11. 2012 23:57)
Re: determinant obecné matice
↑ check_drummer:,
Napadla ma ina metoda, inspirovanou zo slavnej knihy Polya, Szego; Problem and Theorem in Analysis II
Najprv sa dokazat, ze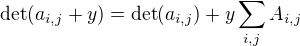
kde  je kofaktor
je kofaktor  matice
matice 
Dokaz:
Najprv sa budem zaoberat determinantom
 ktoreho cleny su
ktoreho cleny sua1 b b ... b
a a2 b ... b
a a a3 ... b
. . . .
. . . .
a a a an
Je jednoduche konstatovat, ze

a

Eliminacia
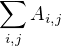 da:pre
da:pre 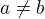

Ak
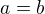 , (akoze det je spojita funkcia
, (akoze det je spojita funkcia  jeho koeficientov,a naviac je to polynom z
jeho koeficientov,a naviac je to polynom z  neznamymy (variables).
neznamymy (variables).Tak fixujme
 a hladajme limitu najdeneho vyrazu pre
a hladajme limitu najdeneho vyrazu pre  , co sa priblizuje k
, co sa priblizuje k  :
: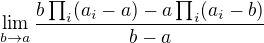 , co vlastne je derivacia
, co vlastne je derivacia  v bode
v bode  (premenna b)
(premenna b)Cize mame
 (pre
(pre 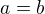 )
)Poznamka:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 10. 11. 2012 08:53
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
↑ check_drummer:
Pokud jedno  bude rovno
bude rovno  , ještě to neznamená, že determinant bude nulový.
, ještě to neznamená, že determinant bude nulový.
Offline
#18 10. 11. 2012 14:02
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: determinant obecné matice
↑ vanok:
Myslím, že místo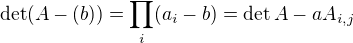
by mělo být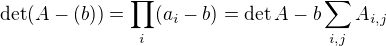
a podobně o řádek výš chybí znak sumy, ale to ses asi jen přepsal, jinak mi přijde řešení v pořádku. Pěkné :-).
Offline
#19 10. 11. 2012 14:26 — Editoval vanok (10. 11. 2012 14:47)
Re: determinant obecné matice
↑ Pavel Brožek:, dakujem za precitanie prispevku. Ano mas pravdu z tym suctom. Reeditujem to hned.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 10. 11. 2012 20:19
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: determinant obecné matice
↑ Pavel Brožek:
Díky, už mi to asi v noci nemyslelo, upravím.
"Máte úhel beta." "No to nemám."
Offline
#21 10. 11. 2012 23:23
- check_drummer

- Příspěvky: 4638
- Reputace: 99
Re: determinant obecné matice
↑ vanok:
Ahoj, mohl bys prosím trošku více rozepsat důkaz tvrzení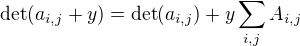
? (Hide jsem si otevřel, ale nevidím, jak ten vztah z linearity determinantu plyne. Předpokládám, že más na mysli linearitu vzhledem k nějakému řádku/sloupci.)
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#22 11. 11. 2012 00:12
Re: determinant obecné matice
↑ check_drummer:,
Ak to takto nevidis, skus napisat 8 matric linearnych podla stlpcou, ako som ta tam poradil...a som isty ze to okamzite pochopis.
Inac v poslednej poznamke, som dal este iny (nepresnejsi, ale dostatocny) dokaz, podla indikacie v knihe od Polya.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 11. 11. 2012 15:45
Re: determinant obecné matice
Ahoj ↑ Honza90:,
Tak nam napis aspon vysledky tvojej prace.
Co, napriklad pisal ja, ti da aj metodu na ine vypocty.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1 2
- Hlavní strana
- » Zajímavé úlohy z algebry
- » determinant obecné matice (TOTO TÉMA JE VYŘEŠENÉ)
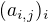 a druhu len z
a druhu len z  nam da
nam da 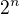 determinantov, z ktorych nenulove su prave
determinantov, z ktorych nenulove su prave 
 .
.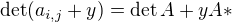 kde
kde 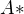 neobsaduje ziadne
neobsaduje ziadne  ?
?