Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 11. 2012 17:32
Diferenciální rovnice
Dobrý den,
řeším následující diferenciální rovnici:  .
.
Substitucí  jsem ji převedl na rovnici
jsem ji převedl na rovnici  , ale tato rovnice není exaktní, homogenní, ani zde nejde nějakým způsobem separovat proměnné.
, ale tato rovnice není exaktní, homogenní, ani zde nejde nějakým způsobem separovat proměnné.
Nemáte někdo nápad, jak pokračovat?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 23. 11. 2012 17:49
Re: Diferenciální rovnice
↑ Sulfan: Ahoj!
Náš kamarát stroj to označil za Bernoulliho rovnicu, pozri step-by-step
http://www.wolframalpha.com/input/?i=z% … x^4%29%3D0
Offline
#3 23. 11. 2012 20:34 — Editoval Tomas.P (23. 11. 2012 20:41)
Re: Diferenciální rovnice
↑ Sulfan:
Postup (http://mi21.vsb.cz/sites/mi21.vsb.cz/fi … ovnice.pdf):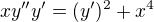 , substituce:
, substituce: 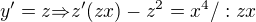
(1) 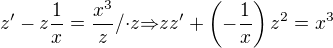 ,
,
substituce: 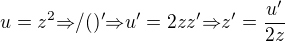 ,
,
dosazení do (1): 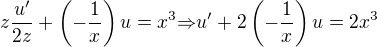 ,
,
Bernoulliova dif. rce přechází do dif. rce 1.řádu ve tvaru: 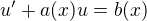 , kde
, kde 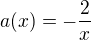 ,
, 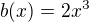 , roznásobím dif. rce 1.řádu
, roznásobím dif. rce 1.řádu 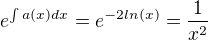 a dostávám:
a dostávám: 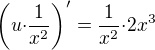
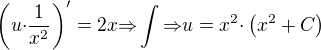 ,
,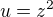 proto:
proto: 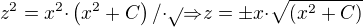 , dále
, dále 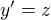 proto:
proto: 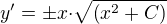 a po integraci vychází:
a po integraci vychází: 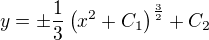 .
.
Offline
#4 23. 11. 2012 21:03
Re: Diferenciální rovnice
↑ pietro: Děkuji, bohužel zde nejsem registrovaný, abych mohl zobrazit postup řešení.
↑ Tomas.P: Díky, to vydělení tím zx byl zřejmě klíčový krok, pak mi to je naprosto jasné. Uděluji bodík :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)