Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » průběh fce s parametrem (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 12. 2012 12:31
průběh fce s parametrem
Ahoj, nemám dotaz spíš bych potřebovala poradit, jestli nevíte kde se dají sehnat nejlépe řešené příklady na průběh funkci s parametrem? hledala jsem na internetu i v učebnicích, ale nikde jsem nic nenašla. děkuji předem;-)
Offline
- (téma jako vyřešené označil(a) simcilka)
#2 28. 12. 2012 13:00
Re: průběh fce s parametrem
Mám třeba zadaný příklad  , kde
, kde  rozdělila jsem to na c<0, c=0 a c>0 a pocítala jsem to pro každý případ zvlášť, ale nevím jak korektně zapsat když c=0 protože to mi vyjde konstantní fce kt. má definicni obor
rozdělila jsem to na c<0, c=0 a c>0 a pocítala jsem to pro každý případ zvlášť, ale nevím jak korektně zapsat když c=0 protože to mi vyjde konstantní fce kt. má definicni obor  , ale jak mám napsat derivace a tak???
, ale jak mám napsat derivace a tak???
Offline
#3 28. 12. 2012 13:31
Re: průběh fce s parametrem
Ahoj.
O literatuře na dané tema nic nevím, ale zkusím poradit s tím konkretním dotazem, pokud jsem ho pochopil správně.
Je vhodné upravit funkci na co nejpříhodnější tvar, zde
 ,
,
takže
 ,
,
odtud je vidět , že pro  a přípustná
a přípustná  je
je  , což v souladu s faktem, že jde o konstantní funkci.
, což v souladu s faktem, že jde o konstantní funkci.
Offline
#4 01. 01. 2013 19:42
Re: průběh fce s parametrem
jj, děkuji, tak jsem to tak napsala, ale nebyla jsem si jistá jestli je to korektní zápis. Mohla bych ještě konzultovat jeden příklad na vyšetřění průběhu fce s paramterem?
zadaní  , kde a je parametr
, kde a je parametr 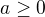
moje řešení: pro 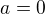 by vyšla odmocnina ze záporného čísla, takže tato fce na reálných číslech není definovana
by vyšla odmocnina ze záporného čísla, takže tato fce na reálných číslech není definovana
pro  musí být splněna podmínka, že
musí být splněna podmínka, že 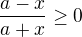 a to je bud
a to je bud  nebo
nebo  no a ted nevím jak to mám řešit dál, protože nevím jak zapsat definiční obor, a podle mých výpočtů limita v nekonečnu neexistuje,.. pomužete prosím? děkuji
no a ted nevím jak to mám řešit dál, protože nevím jak zapsat definiční obor, a podle mých výpočtů limita v nekonečnu neexistuje,.. pomužete prosím? děkuji
Offline
#5 02. 01. 2013 09:37 — Editoval Rumburak (02. 01. 2013 09:42)
Re: průběh fce s parametrem
↑ simcilka:
Začal bych základním předpokladem
(1)  ,
,
aby měl smysl ten zlomek.
Pro  vynásobíme nerovnost
vynásobíme nerovnost 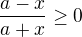 vvýrazem
vvýrazem  , který je dle (1) větší než 0, a tím dostaneme
, který je dle (1) větší než 0, a tím dostaneme 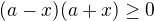 ,
,  ,
,  ,
, ![kopírovat do textarea $x \in (-a, a]$](/mathtex/d9/d90e7c9656508f02bad73fecf4713c6d.gif) (opět použito (1)).
(opět použito (1)).
Definičním oborem funkce  pro
pro  je tedy interval
je tedy interval ![kopírovat do textarea $(-a, a]$](/mathtex/f5/f506ceb0fe265437d1dc3aff3f483dd6.gif) .
.
Offline
#6 02. 01. 2013 15:48
Re: průběh fce s parametrem
↑ Rumburak:
dekuji, ja jsem se nakonec k tomuto taky dopočítala pres tohle 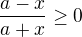 a rozkladala jsem si to, protoze jsem nechtela spekulovat nad tim co je vetsi nebo mensi nez nula.
a rozkladala jsem si to, protoze jsem nechtela spekulovat nad tim co je vetsi nebo mensi nez nula.
ten napad vynasobit to  by me nenapadlo, děkuji to jsme si už poznačila a mohu jeste pozadat o kontrolu, konce?
by me nenapadlo, děkuji to jsme si už poznačila a mohu jeste pozadat o kontrolu, konce?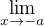 je nekonecno,
je nekonecno,  je nula, derivace =
je nula, derivace =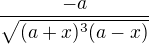 , takze def obor derivace je (-a,a) a stacionarni bod je a. a ted nevim jak mam napsat kde je fce rostouci a klesajici, vyslo mi, ze pro menzi nez a bude klesajici a pro vetsi rostouci a ze v a je lokalni min? je to spravne? a dale jsem jeste pocitala
, takze def obor derivace je (-a,a) a stacionarni bod je a. a ted nevim jak mam napsat kde je fce rostouci a klesajici, vyslo mi, ze pro menzi nez a bude klesajici a pro vetsi rostouci a ze v a je lokalni min? je to spravne? a dale jsem jeste pocitala 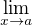 zprava zleva derivace a to mi vyšlo že neex.
zprava zleva derivace a to mi vyšlo že neex.
dekuji
Offline
#7 02. 01. 2013 16:42
Re: průběh fce s parametrem
↑ simcilka:
Pozor na to, že limity v krajních bodech intervalu, který je definičním oborem funkce, nutno uvažovat pouze jako jednostranné.
Jejich hodnoty máš správně.
Derivace mi vyla také tak. Avšak pro  má všude zápornou hodnotu (stacionární bod funkce
má všude zápornou hodnotu (stacionární bod funkce  , v němž by měla
, v němž by měla
její derivace hodnotu 0, tedy neexistuje).
Výsledek  v
v  znamená, že funkce
znamená, že funkce  je v tomto intervalu klesající. V bodě
je v tomto intervalu klesající. V bodě  je spojitá zleva,
je spojitá zleva,
proto z předchozího vyplývá, že v tomto bodě nabývá svého jediného lokálního (a zároveň absolutního) minima.
Jiných extrémů na svém def. oboru nemá.
Odpovídající jedostranné limity derivace v krajních bodech existují, ale jsou nevlastní (v obou případech  ).
).
Offline
#8 02. 01. 2013 21:02
Re: průběh fce s parametrem
↑ Rumburak:
děkuji již jsem si to opravila;-) dále mi vyšlo že je konkávní na D(f) a obor hodnot je (0, nekonecno)
Offline
#9 03. 01. 2013 11:19 — Editoval Rumburak (03. 01. 2013 11:19)
Re: průběh fce s parametrem
↑ simcilka:
Mně vyšlo, že druhá derivace mění znaménlo v bodě 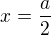 , napravo je záporná a nalevo kladná.
, napravo je záporná a nalevo kladná.
Mohl jsem se přepočítat, ale Tvůj výsledek, že funkce je konkávní na celém 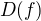 , je na první pohled nesprávný.
, je na první pohled nesprávný.
Zkus si nakreslit funkci, která je na omezeném intervalu klesající, konkávní a v levém krajním bodě jde zprava do  .
.
Určitě se Ti to nepodaří.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » průběh fce s parametrem (TOTO TÉMA JE VYŘEŠENÉ)