Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 01. 2013 00:09
Re: Integral pod odmocninou
Ahoj,
my na to používáme Eulerovy substituce viz zhruba v půlce stránky. :)
Offline
#3 04. 01. 2013 01:39
Re: Integral pod odmocninou
Ahoj,
buď univerzální Euler, jak psal kolega.
Druhý se dá také řešit vytknutím x před odmocninu, následuje substituce 1/x, doplnění na čtverec a úpravu na integrál 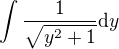 , který se dá spočítat hyperbolickou substitucí (je to derivace hyperbolické funkce).
, který se dá spočítat hyperbolickou substitucí (je to derivace hyperbolické funkce).
První by mohl jít po doplnění na čtverec pomocí per partes upravit na podobný druhému.
Offline
#4 04. 01. 2013 12:07 — Editoval Gresthorn (04. 01. 2013 12:08)
Re: Integral pod odmocninou
Ten druhý aj vyšiel pomocou eulerových substitúcií, no ten prvý nie :(
Skúšal som aplikovať eulerovú substitúciu, ale všimol som si, že na tejto stránke (niekde za polovicou stránky) je navyše aj tá kvadratická časť spolu s odmocninou v substitúcii.
Položil som tak:
odkiaľ mi vyšlo, že: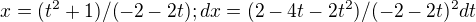
Dostal som tak integrál, ktorý sa ale podľa tohoto výsledku nezhoduje so skutočným výsledkom.... Neviete mi poradiť, kde som spravil chybu? Skontroloval som si to po sebe, ale asi stále niečo prehliadnem :(
Offline
#5 05. 01. 2013 02:24 — Editoval 010010 (05. 01. 2013 02:42)
- 010010

- Příspěvky: 82
Re: Integral pod odmocninou
↑ Gresthorn:
Ahoj.
Nezávisle na tebe, mám postup taký istý. Akurát substitúciu nemám (x+1) ale (x+t). Ale myslím že stačí len pokračovať.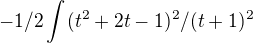
Čiže po upravení máme: 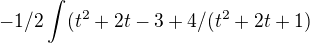
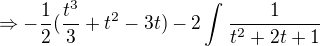
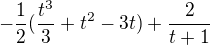
Už len dosadiť
Offline
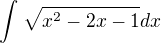
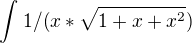
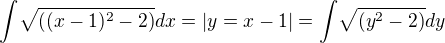 , ale úprava pomocí per partes ne. Předem děkuji za odpověď
, ale úprava pomocí per partes ne. Předem děkuji za odpověď