Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 01. 2013 18:27
Integrál
Dobrý den, řeším integrál (sin x)^n dx. Nějak jsem se do toho zamotala tak, že už ani nevím co dělám.. :( Kdyby se jednalo jen o integrál x^n, byla by primitivní funkce (x^(n+1))/(n+1), to je jasný, ale když je to složená funkce, nevím si s tím rady. Poradí mi prosím někdo? Aspoň způsob. Zkoušela jsem substituci, ale neúspěšně.
Offline
- (téma jako vyřešené označil(a) jelena)
#4 04. 01. 2013 19:12
Re: Integrál
Ne, půjčení si jednoho sinu.
Offline


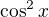 , se tam objevit má, po rozepsání na
, se tam objevit má, po rozepsání na 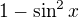 , by se měl objevit kýžený rekurentní vztah.
, by se měl objevit kýžený rekurentní vztah.