Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Rozklady uspořádaných množin na (anti)řetězce. (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 01. 2013 15:15 — Editoval Andrejka3 (17. 01. 2013 12:42)
Rozklady uspořádaných množin na (anti)řetězce.
Dobrý den.
Podobnost tvrzení okolo existencí minimálních (disjunktních) rozkladů konečných uspořádaných množin na řetězce, resp. antiřetězce mě navedla k některým nejasným otázkám.
Buď  uspořádaná konečná množina. Buď
uspořádaná konečná množina. Buď 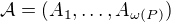 její (minimální) rozklad na antiřetězce. Uspořádejme antiřetězce z
její (minimální) rozklad na antiřetězce. Uspořádejme antiřetězce z  podle mohutnosti a označme
podle mohutnosti a označme 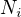 počet antiřetězců z rozkladu, jež mají mohutnost
počet antiřetězců z rozkladu, jež mají mohutnost  , kde stačí vzít
, kde stačí vzít 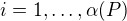 .
.
Dostaneme posloupnost 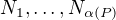 , tak že
, tak že 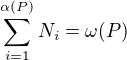
1) Je 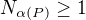 ?
?
Vyřešeno v ↑ Andrejka3:, odpověď
2) Jak moc dobře tato posloupnost charakterizuje uspořádanou množinu? Tak například, kolik neizomorfních uspořádaných množin má posloupnost (1,2)?
3) Existuje uspořádaná množina, která má aspoň dva různé minimální rozklady dávající různé posloupnosti?
Vyřešeno v ↑ Andrejka3:, odpověď
Otázky 4,5,6 v dalších dvou příspěvcích.
Analogicky pro rozklad na řetězce. Jsou to triviální otázky, nebo kolem toho existuje teorie? (Když tak se to dá přesunout do sekce VŠ).
Značení, definice, věty:
rozkladem množiny mám na mysli dusjunktní systém jejích neprázdných podmnožin, který ji pokrývá.
alfa, omega:
Věty o rozkladech (některé nejsou přímo převzaté, ale dělala jsem důkazy)
na antiřetězce:
na řetězce:
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 15. 01. 2013 21:38 — Editoval Andrejka3 (18. 01. 2013 16:48)
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Nevěděla jsem, kdy a jestli vůbec nějakou otázku vyřeším.
ad 1,3:
Je znám algoritmus pro konstrukci rozkladu P do antiřetězců:
Zkonstruujeme
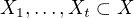 pomocí algoritmu:
pomocí algoritmu:
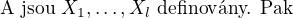

4) Takto dostaneme minimální rozklad (právě
 antiřetězců). Je v tomto rozkladu nutně antiřetězec s mohutností
antiřetězců). Je v tomto rozkladu nutně antiřetězec s mohutností  ?
?Vyřešeno v ↑ Andrejka3:, odpověď:
5) Existuje algoritmus pro nalezení minimálního rozkladu na řetězce? Edit: něco lepšího než projít všechny možnosti.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 15. 01. 2013 22:33 — Editoval Andrejka3 (17. 01. 2013 12:46)
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
ad 4:
6) Pro každou poset, konečnou existuje minimální rozklad na antiřetězce, který obsahuje antiřetězec mohutnosti
 .
.Vyřešeno v ↑ Andrejka3:, odpověď:
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 16. 01. 2013 20:35
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Ahoj, ad 5) Ano, ale asi Ti jde o nějaký algoritmus, který neprochází všechny možnosti, že?
"Máte úhel beta." "No to nemám."
Offline
#5 16. 01. 2013 20:52
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ check_drummer:
Ahoj, ano. Měla jsem to specifikovat. Ale pokud máš nějaký míň brutální než udělej všechny možné rozklady do  množin, budu za něj ráda.
množin, budu za něj ráda.
Je to zvláštní. Když máme Hasse diagram, je jednoduché použít ten algoritmus na rozklad do antiřetězců, protože minimální prvky se hledají snadno.
A myslíš si něco o 6)?
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 16. 01. 2013 22:15
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Ad 6) zatím nevím. :-)
Ad 5) A co třeba hladový algoritmus? Začni s nějakým minimálním prvkem a prodlužuj řetězec libovolně dokud to lze. Tím získáš řetězec. Stejným způsobem tvoř další řetězce, dokud je to možné. Ani jsem se ale nepokoušel dokázat správnost ani najít protipříklad.
"Máte úhel beta." "No to nemám."
Offline
#7 16. 01. 2013 22:34
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Jen takový nápad:
Pokud mám nějaký maximální antiřetězec B a v nějakém minimálním rozkladu na antiřetězce se bude vyskytovat B (resp. jeho prvky) v aniřetězcích B1,..,Bk, pak pokud vezmu B1 a jako Ci (i=2,..,k) označím ty prvky z B1, které jsou porovnatelné s Bi. pak bych mohl v B1 zaměnit prvky Ci a Bi (pokud se nějaký prvek vyskytuje ve více Ci, pak ho zařadím jen do jednoho Bi). Přesněji - zaměnit prvky zanmená vyměnit je mezi jimi odpovídajícími antiřetězci. Po této záměně tedy bude B1 obsahovat všechna Bi, tj. celý B.
Otázka je, zda je to postup korektní.
"Máte úhel beta." "No to nemám."
Offline
#8 16. 01. 2013 23:12 — Editoval Andrejka3 (16. 01. 2013 23:25)
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ check_drummer:
Zajímavý nápad!
Zkoušela jsem si ověřit, jestli rozumím tomu postupu.
Existuje jediný 3 prvkový antiřetězec. Ten je obsažen v červeném a modrém antiřetězci - B_1 a B_2.
C_2 = modrá kulička nahoře. Tu obarvím na červeno a ty spodní dvě na modro.
Skvělé je, že takto opravdu získám opět antiřetězce.
Vždy musí dojít k netriviální výměně, jinak by ty dva antiřetězce šly sjednotit do jednoho, že? To by byl spor s minimalitou rozkladu.
Edit: Budu o tom přemýšlet. Jsem moc ráda, žes o tom přemýšlel.
Myslím, že to je dobře. :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 16. 01. 2013 23:29
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Ještě je potřeba to doladit - ve Tvém případě bys také mohla začít s dvěma červenými prvky jako B1 a pak bys už neměla je za co vyměnit s tím modrým (B2) vpravo dole (tentokrát bychom sestavovali maximální antiřetězec v červené barvě). Ale to prostě vyřešíme tak, že je-li Ci prázdná, tak prostě Bi přesuneme do B1 bez výměny. Spor s minimalitou rozkladu to není, protože minimalita rozkladu a minimalita délky konkrétního antiřetězce jsou dvě různé věci.
Nerozumím Tvé otázce:
"Proč ale musí k sobě přijít ty prvky onoho maximálního antiřetězce...?"
"Máte úhel beta." "No to nemám."
Offline
#10 16. 01. 2013 23:41
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ check_drummer:
Jo, to jsem editovala pryč. Musím si to promyslet, jsem pomalá.
What does a drowning number theorist say?
'log log log log ...'
Offline
#11 17. 01. 2013 12:03 — Editoval Andrejka3 (18. 01. 2013 16:43)
Re: Rozklady uspořádaných množin na (anti)řetězce.
Ad 6)
Teď už zbývá jen slušný algoritmus na rozklad do řetězců a dokázat analogická tvrzení pro "anti objekty". Předpokládám, že to vyjde stejně - ale kdo ví. Pro úplnost to asi dodělám.
↑ check_drummer: Hladový algoritmus neznám. Tyhle věci neovládám (ale vyhledat si to můžu..). Díky za nápady!
Edit: Byla bych klidnější, kdyby někdo potvrdil správnost těch vět na začátku. Ještě to je pro mě novinka a asi bych dostala infarkt, kdybych tam po pár měsících našla chybu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 18. 01. 2013 16:51
Re: Rozklady uspořádaných množin na (anti)řetězce.
Řešení 6) ještě nabídlo další záhadu, ale to už možná zacházím moc daleko.
Kdyby někoho ještě něco napadlo, nebo měl otázky, prosím, neváhejte napsat. Jinak, na hlavní otázky mám odpovědi, takže téma označím jako vyřešené.
What does a drowning number theorist say?
'log log log log ...'
Offline
#13 18. 01. 2013 20:00 Příspěvek uživatele check_drummer byl skryt uživatelem check_drummer. Důvod: Už vidím reakci.
#14 18. 01. 2013 20:04 — Editoval check_drummer (18. 01. 2013 20:11)
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Hladový alg. bere co nejvíc může a moc neplánuje. :-) Takže poté co zvolím libovolný maximální řetězec, tak ho odstraním a dále vyberu další řetězec stejným způsobem, tak pokračuju dokud nenajdu celý rozklad.
Ale vidím, že máš protipříklad... Možná by tedy bylo vhodné volit takový řetězec, na který je "napojeno" co nejméně dalších prvků...
"Máte úhel beta." "No to nemám."
Offline
#15 21. 01. 2013 10:54 — Editoval Andrejka3 (21. 01. 2013 11:29)
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ check_drummer: Díky za milé vysvětlení :)
K těm posets, které nemají minimální rozklad s "největším (anti)řetězcem". Vlastně jsem to pozorování už učinila, ale nenapsala ho.
Umluva / omluva: Zaměňuji mezi sebou nosnou množinu X a název struktury P, jak mi to přijde pod ruku.
Edit: nějaké úvahy. Vyplynula z nich charakterizace množin, jež nemají mini. rozklad s max objektem.
Buď
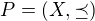 poset, konečná. Označme
poset, konečná. Označme  systém všech antiřetězců s mohutností
systém všech antiřetězců s mohutností 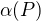 . Platí:
. Platí:analogicky, ctrl+c, ctrl+v
Buď
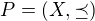 poset, konečná. Označme
poset, konečná. Označme  systém všech řetězců s mohutností
systém všech řetězců s mohutností 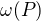 . Platí:
. Platí:What does a drowning number theorist say?
'log log log log ...'
Offline
#16 21. 01. 2013 11:59 — Editoval Andrejka3 (23. 01. 2013 13:06)
Re: Rozklady uspořádaných množin na (anti)řetězce.
↑ Andrejka3:
Jaké podstruktury musí nutně mít posets, které nemají minimální rozklad do antiřetězců s antiřet. s moh.  ?
?
1)  .
.
2)Volme 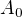 antiřetězec,
antiřetězec, 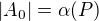 .
.
3) Dle charakterizace v předchozím příspěvku existuje  řetězec,
řetězec, 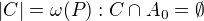 .
.
Označme 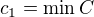 ,
,  .
.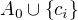 není antiřetězec, tedy existuje
není antiřetězec, tedy existuje 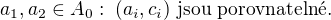
Jistě musí být  a
a  .
.
Kdyby 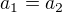 , z maximality
, z maximality  musí být
musí být 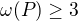 . Nyní můžeme postupovat po bezprostředních následnících řetězce. Tak pro
. Nyní můžeme postupovat po bezprostředních následnících řetězce. Tak pro  plyne, že nemůže být
plyne, že nemůže být 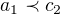 , byl by to spor s maximalitou řetězce. Musí být buďto
, byl by to spor s maximalitou řetězce. Musí být buďto 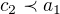 anebo jsou neporovnatelné. Kdyby ovšem
anebo jsou neporovnatelné. Kdyby ovšem 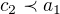 , můžeme stejně argumentovat pro
, můžeme stejně argumentovat pro 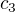 . Takhle se lze dostat až k
. Takhle se lze dostat až k 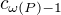 , kde ovšem již nemáme jinou možnost než aby byly
, kde ovšem již nemáme jinou možnost než aby byly  neporovnatelné. Souhrnně,
neporovnatelné. Souhrnně,  .
.
Stejně lze postupovat zvrchu dolů, takže dostaneme  . Je
. Je  a tak (opět z maximality řetězce) rovněž existuje něco mezitím,
a tak (opět z maximality řetězce) rovněž existuje něco mezitím,  . Pak
. Pak  je neporovnatelné s
je neporovnatelné s  . Do P pak lze vnořit struktura
. Do P pak lze vnořit struktura
Kdyby  , pak musí poset obsahovat strukturu
, pak musí poset obsahovat strukturu
Tady je problém s barevnými čarami. O nich nic nevím. Pokud tam je aspoň jedna, pak lze převést na případ první. Pokud není ani jedna, nutno řešit zvlášť: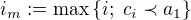 ,
,  . Z nezávislosti
. Z nezávislosti  plyne
plyne  , tedy do P lze vnořit
, tedy do P lze vnořit
Přidám jen ještě, že  je nutná podmínka pro to, aby poset neměla min rozklad s max antiř. To je intuitivní.
je nutná podmínka pro to, aby poset neměla min rozklad s max antiř. To je intuitivní.
Ke spokojenosti chybí vyvrátit domněnku o vnoření M_3 a N_5 nějakým protipříkladem.
Závěr: Poset nemá min. rozklad do antiř. obsahující alfa antiřet, pak aspoň jedna z dvou struktur (bez barevných čar) do ní lze vnořit.
Edit: Update.
Edit: Úplně stejnou věc dostanu pro rozklady na řetězce, protože z těch charakterizačních tvrzení jsem použila pouze existenci dvojice A,C antiř a řet s mohutností alpha, resp omega takové, že mají prázdný průnik. Jak využít tvrzení v celém znění, to nevím.
What does a drowning number theorist say?
'log log log log ...'
Offline
#17 22. 01. 2013 13:36 — Editoval Andrejka3 (22. 01. 2013 14:35)
Re: Rozklady uspořádaných množin na (anti)řetězce.
Myslím, že docela zajímavý update ohledně podstruktur v předchozím příspěvku.
Hlavní výsledek je charakterizace posets, které nemají rozklad do minim. antiřetězců s \alpha(P)-prvkovym antiřetězcem a jeji analogie pro retezce.
Podstruktury, které jsem dostala a které musí obsahovat každá taková poset (neexistence min rozk do anti. s alfa antir.) jsou moc titěrné. Kromě toho je to jen nutná podmínka, takže to je chabé.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Rozklady uspořádaných množin na (anti)řetězce. (TOTO TÉMA JE VYŘEŠENÉ)


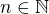 ,
, 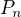 n prvková poset,
n prvková poset,  na antiřetězce.\\
na antiřetězce.\\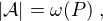

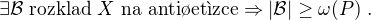
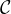 rozklad
rozklad 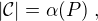
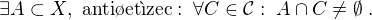
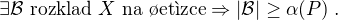
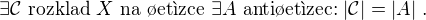
 .
.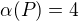
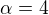 modre
modre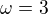
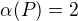 ,
, 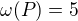 . Pokud vezmu jediný pětiprvkový řetězec, zbude
. Pokud vezmu jediný pětiprvkový řetězec, zbude  -prvkový antiřetězec, tedy rozklad obsahující tento řetězec není minimální. Je náhoda, že do prvního, resp.~druhého protipříkladu lze vnořit svaz
-prvkový antiřetězec, tedy rozklad obsahující tento řetězec není minimální. Je náhoda, že do prvního, resp.~druhého protipříkladu lze vnořit svaz 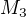 , resp.~
, resp.~ ?
?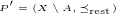 , kde
, kde 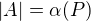 platí:
platí:  , neboli "odebráním antiřetězce nezmenším původní výšku".
, neboli "odebráním antiřetězce nezmenším původní výšku".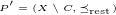 , kde
, kde 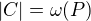 platí:
platí:  , neboli "odebráním řetězce nezmenším původní šířku".
, neboli "odebráním řetězce nezmenším původní šířku".