Matematické Fórum

010010 · 25. 01. 2013 02:37 — Editoval 010010 (25. 01. 2013 02:47)

Dobrý večer,

Lineárne zobrazenie: $Z: R^6 -> R^3$

$|x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}|$
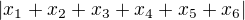
Také že : 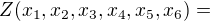$Z(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})=$ $| x_{1}+x_{3}+x_{5} |$
$| x_{2}+x_{4}+x_{6} |$

Definiciu jadra aj obrazu poznam. Skúste ma trošku nasmerovať prosím.

kompik · 25. 01. 2013 06:20 — Editoval kompik (25. 01. 2013 06:23)

↑ 010010:
Myslim, ze podobnych prikladov najdes na tomto fore viacero uz vyriesenych:
Google: jadro obraz site:matweb.cz

Dokonca je takato tema aj v sekcii vzorove priklady: http://forum.matweb.cz/viewtopic.php?id=650

Malo by Ti vyjst, ze sucet dimenzie jadra a dimenzie obrazu je 6.
Wikipedia: Rank-nullity theorem

Rumburak

↑ 010010:
Zdravím .

Poněkud Ti nerozumím.

Máš-li nalézt jádro toho zobrazení a znáš-li definici jádra, tak bys měl též vědět, že nalézt jádro znamaná vyřešit rovnici (resp. soustavu)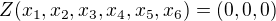
$Z(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})= (0, 0, 0)$ , to je přesně v souladu s definicí jádra.

S tím obrazem to bude obdobné - nalézt obraz znamená nalézt všechny hodnoty parametrů 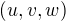$(u, v , w)$ tak, aby soustava
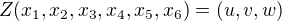$Z(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})= (u, v , w)$ byla řešitelná. Opět jsem de facto jen zopakoval definici. Zde ale můžeme též využít
znalost jádra a úlohu zjednodušit.

Možná jsi chtěl dotaz zformulovat "není mi jasné, jak řešit soustavy lineárních rovnic (závislé na parametrech)".

PS. U této úlohy nejpíš půjde využít, že

$x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} = (x_{1} + x_{3} + x_{5}) + (x_{2} + x_{4}+ x_{6})$ ,

což umožní vnímat zobrazení 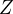$Z$ jako komposici jiných a jednodušších lineárních zobrazení.

Matematické Fórum

#1 25. 01. 2013 02:37 — Editoval 010010 (25. 01. 2013 02:47)

Jadro a obraz lineárneho zobrazenia.

#2 25. 01. 2013 06:20 — Editoval kompik (25. 01. 2013 06:23)

Re: Jadro a obraz lineárneho zobrazenia.

#3 25. 01. 2013 09:59 — Editoval Rumburak (25. 01. 2013 10:11)

Re: Jadro a obraz lineárneho zobrazenia.

Zápatí