Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 30. 01. 2013 22:08
Re: Permutace příklad
↑ Matiniela:
Ze zadání vidíme, že sestavujeme pěticiferné číslo z pěti cifer, takže n=k, takže využijeme permutaci. V zadání požadují, že čísla se nesmí opakovat. Takže permutace bez opakování.
Nejprve požadují, abychom určili počet všech pěticiferných čísel z cifer 0, 1, 4, 7, 9.
Takže počet bude 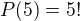 , jenomže v cifrách se vyskytuje číslo
, jenomže v cifrách se vyskytuje číslo  a musíme tedy odečíst možnosti, kde čísla začíná nulou (je jasné, že číslo 04197 je stejné jako 4197, takže možnosti, kde nula je na začátku, odečteme).
a musíme tedy odečíst možnosti, kde čísla začíná nulou (je jasné, že číslo 04197 je stejné jako 4197, takže možnosti, kde nula je na začátku, odečteme).
Takže si sestavíme 0 X X X X ... na začátku je nula, za X dosazujeme 1, 4, 7 a 9, teda takových čísel je 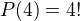 ...
...
Nyní určíme celkový počet pěticiferných čísel 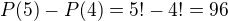 .
.
Dále se nás ptají, kolik jich je sudých. Sudá čísla jsou čísla, která koční 0, 2, 4, 8. Naší podmínce vyhovují čísla 0 a 4.
Nejprve určíme počet čísel, kde nula se vyskytuje na konci, tedy ... X X X X 0 - za X dosazujeme 1, 4, 7 a 9, tedy počet takových čísel je 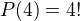
Dále určíme počet čísel, kde čtyřka se vyskytuje na konci, tedy ... X X X X 4 - za X dosazujeme 1, 0, 7 a 9, tedy počet takových čísel je 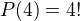 ... jenomže máme opět situaci, že nula může být na začátku, tedy musíme odečíst možnosti, kde nula je na začátku ... tedy získáme 0 X X X 4 .. za X dosazujeme 1, 7 a 9, tedy počet takových čísel je
... jenomže máme opět situaci, že nula může být na začátku, tedy musíme odečíst možnosti, kde nula je na začátku ... tedy získáme 0 X X X 4 .. za X dosazujeme 1, 7 a 9, tedy počet takových čísel je 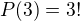
Z toho všeho tedy usoudíme, že celkový počet sudých čísel je 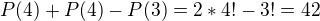
Snad to z toho pochopíš ... já to chápu, teď záleží, jestli jsem to podala ve vyhovující podobě ...
Offline

