Matematické Fórum

jarrro · 01. 02. 2013 13:58 — Editoval jarrro (01. 02. 2013 13:59)

ahojte na základe tjeto témyhttp://forum.matweb.cz/viewtopic.php?pid=338356
ma napadlo či náhodou neplatí, že pre každú postupnosť a pre ktorú je
$\lim_{n\to\infty}{a_n}=0$
existuje rastúca postupnosť n prirodzených čísel taká, že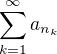
$\sum_{k=1}^{\infty}{a_{n_k}}$
je konvergentný rad
ak postupnosť a má nekonečne veľa kladných a súčasne aj nekonečne veľa záporných členov tak by sa vyberali tak aby sa striedali znamienka a znižovala absolútna hodnota čiže tento prípad je (snáď) vyriešený
platí to aj pri radoch ktorých členy od nejakého indexu nemenia znamienko?

Stýv · 01. 02. 2013 14:05

platí, stačí např. brát $n_k$ tak, aby platilo $|a_{n_k}|<2^{-k}$

jarrro · 01. 02. 2013 15:17

↑ Stýv:aha díky potom to bude dokonca absolútne konvergentné

Stýv · 01. 02. 2013 15:33

↑ jarrro: to bejvá, když členy nemění znamínko

jarrro · 01. 02. 2013 15:53

veď hej neuvedomil so si to,ale na druhej strane sa to dá použiť na ľubovoľnú postupnosť a dokazuje to, že z každého radu,ktorý splňuje nutnú podmienku konvergencie sa dá vybrať dokonca absolútne konvergentný podrad je to tak?

Stýv · 01. 02. 2013 16:11

↑ jarrro: a dokonce jeho součet můžeš udělat libovolně malý;)

jarrro · 01. 02. 2013 18:18

↑ Stýv:aha fakt stačí brať členy v absolútnej hodnote menšie ako
$\frac{\varepsilon}{2^k}$ díky

Matematické Fórum

#1 01. 02. 2013 13:58 — Editoval jarrro (01. 02. 2013 13:59)

konvergentný "podrad"

#2 01. 02. 2013 14:05

Re: konvergentný "podrad"

#3 01. 02. 2013 15:17

Re: konvergentný "podrad"

#4 01. 02. 2013 15:33

Re: konvergentný "podrad"

#5 01. 02. 2013 15:53

Re: konvergentný "podrad"

#6 01. 02. 2013 16:11

Re: konvergentný "podrad"

#7 01. 02. 2013 18:18

Re: konvergentný "podrad"

Zápatí