Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 02. 2013 17:41 — Editoval nurv (04. 02. 2013 17:41)
Matice lin. zobrazení, obraz funkce
Ahoj, učím se na zkoušku z algebry, ale zasekl jsem se na jednom příkladu, jehož řešení nenalézám ani v mých zápiscích z přednášek...Mohl by mi tu prosím napsat postup (jednotlivé kroky)?Děkuji moc...
Příklad:
ofocený příklad
Offline
#3 09. 02. 2013 16:27 — Editoval Brano (09. 02. 2013 16:34)
Re: Matice lin. zobrazení, obraz funkce
Mas zobrazenie 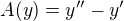 a potrebujes v nom najst obraz bazovych vektorov, teda
a potrebujes v nom najst obraz bazovych vektorov, teda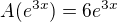 a vyjadrenie tejto funkcie v zadanej baze je
a vyjadrenie tejto funkcie v zadanej baze je 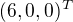 - co je prvy stlpec maticoveho vyjadrenia - podobne zvladnes dalsie stlpce. Staci takto?
- co je prvy stlpec maticoveho vyjadrenia - podobne zvladnes dalsie stlpce. Staci takto?
V b) staci tu maticu prenasobit sprava vektorom co zodpoveda tej fukcii, co je 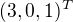
Offline
#4 09. 02. 2013 17:05 — Editoval nurv (09. 02. 2013 17:14)
Re: Matice lin. zobrazení, obraz funkce
Brano napsal(a):
Mas zobrazenie
a potrebujes v nom najst obraz bazovych vektorov, teda
a vyjadrenie tejto funkcie v zadanej baze je
- co je prvy stlpec maticoveho vyjadrenia - podobne zvladnes dalsie stlpce. Staci takto?
V b) staci tu maticu prenasobit sprava vektorom co zodpoveda tej fukcii, co je
Jen, na odkazu není 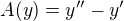 , ale
, ale 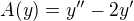
A jak si dostal 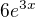 ?
?
A toto 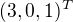 vemu kde?
vemu kde?
V Algebře dost plavu, protože mám od učitele šíleně moc teorie, ale nemáme moc spočítaných příkladů a já se to z teorie nedokážu naučit - musím se učit z praktických postupů...
Díky...
Offline
#5 09. 02. 2013 18:52
Re: Matice lin. zobrazení, obraz funkce
↑ nurv:
Já to zkusím jinak: Je třeba vzít bázové funkce 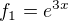 ,
, 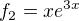 ,
, 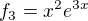 a sestavit funkce
a sestavit funkce 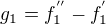 ,
, 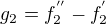 ,
, 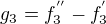 . A pak najít matici A tak, aby platilo g=A.f
. A pak najít matici A tak, aby platilo g=A.f
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#6 09. 02. 2013 18:54
Re: Matice lin. zobrazení, obraz funkce
↑ martisek:
Ještě drobnost: u těch rozdílů g_1, g_2, g_3 chybí dvojka, kterou jsem v zadání zobrazení nějak přehlédl...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#8 09. 02. 2013 20:47
Re: Matice lin. zobrazení, obraz funkce
najdes souradnice techdle "funkci" v puvodnim vektorovem prostoru a tyto souradnice budou radky matice A, protoze pak kdyz matici A nasobime zprava jednotkovyma vektorama puvodni baze (coz jsou f1 f2 a f3) dostaneme prave tyto radky, ktere nam daji zobrazene f1 f2 a f3 pres zobrazeni F
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline

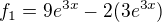
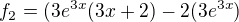
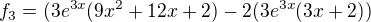
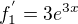 ,
, 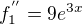
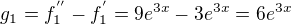

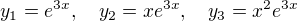
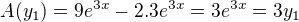
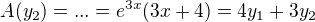
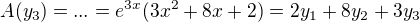
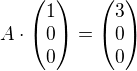
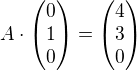
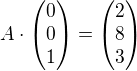

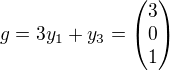
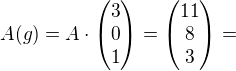
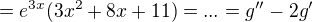
 definované v časti b tvojho zadania.
definované v časti b tvojho zadania.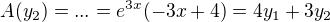
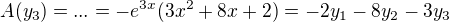
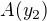 je dobre a
je dobre a 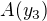 je zle - mas tam opacne znamienko. Pocital som to vo Wolphram|Alpha a tomu vcelku verim, ze sa nemyli.
je zle - mas tam opacne znamienko. Pocital som to vo Wolphram|Alpha a tomu vcelku verim, ze sa nemyli.