Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uzáver množiny - důkaz (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 02. 2013 19:47
uzáver množiny - důkaz
Dobrý večer. Zkontroloval by mi někdo, zda je tento důkaz korektní?
Dokažte, že uzávěr množiny A je nejmenší uzavřená množina obsahující A.
Důkaz:
Předpokládejme, že existuje uzavřená množina  tak, že
tak, že 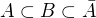 kde
kde 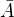 je uzávěr
je uzávěr  .
.
Platí 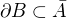 , tedy
, tedy 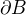 má podle definice uzávěru množiny tyto dvě možnosti:
má podle definice uzávěru množiny tyto dvě možnosti:
a)  čímž je porušen předpoklad, že
čímž je porušen předpoklad, že 
b) 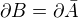 z čehož plyne, že
z čehož plyne, že 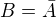
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
- (téma jako vyřešené označil(a) Honza90)
#2 14. 02. 2013 20:37 Příspěvek uživatele Bati byl skryt uživatelem Bati. Důvod: Omyl
#4 14. 02. 2013 22:52
Re: uzáver množiny - důkaz
↑ Honza90:
Napis prosim aku pouzivas definiciu uzaveru a v akom priestore to uvazujes - metricky/topologicky
Offline
#6 14. 02. 2013 23:03
Re: uzáver množiny - důkaz
↑ Honza90:Nech teda existuje uzavreta mnozina  taka, ze
taka, ze 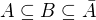 . Nech
. Nech  je vlastna podmnozina mnoziny
je vlastna podmnozina mnoziny 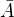 . Potom existuje
. Potom existuje 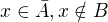 . Nakolko doplnok
. Nakolko doplnok  je otvorena a
je otvorena a  je jej prvkom, tak existuje otvorene okolie bodu
je jej prvkom, tak existuje otvorene okolie bodu  leziace v doplnku
leziace v doplnku  . Dalej je to uz asi jasne, ze?
. Dalej je to uz asi jasne, ze?
Offline
#7 14. 02. 2013 23:06 — Editoval Honza90 (14. 02. 2013 23:11)
Re: uzáver množiny - důkaz
↑ vlado_bb:
No moc ne
To že x má okolí v 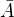 neznamená, že má neprázdný průnik s
neznamená, že má neprázdný průnik s 
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 14. 02. 2013 23:12
Re: uzáver množiny - důkaz
↑ Honza90:Ide o okolie prvku uzaveru mnoziny A, ktore ma s nou prazdny prienik. A taky prvok predsa v uzavere byt nemoze.
Offline
#9 14. 02. 2013 23:14
Re: uzáver množiny - důkaz
↑ vlado_bb:
jasně, už chápu. a co ten můj způsob, je taky správně?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#10 14. 02. 2013 23:16
#11 14. 02. 2013 23:24
Re: uzáver množiny - důkaz
↑ vlado_bb:
Množina hraničních bodu množiny B
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#12 14. 02. 2013 23:31
Re: uzáver množiny - důkaz
↑ Honza90:V casti b pouzivas uvahu 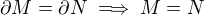 , co ale nie je pravda, napriklad v realnych cislach pri obvyklej metrike je
, co ale nie je pravda, napriklad v realnych cislach pri obvyklej metrike je  , pricom tieto mnoziny su dokonca disjunktne.
, pricom tieto mnoziny su dokonca disjunktne.
Offline
#13 14. 02. 2013 23:45 — Editoval Honza90 (14. 02. 2013 23:45)
Re: uzáver množiny - důkaz
↑ vlado_bb:
stačilo by místo toho říct, že pokud 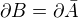 pak neplatí
pak neplatí  ?
?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#14 14. 02. 2013 23:49
Re: uzáver množiny - důkaz
↑ Honza90:Toto moze aj nemusi byt pravda. V priklade s racionalnymi cislami, ktory som uviedol, je to tak, ako pises. Ale napriklad ak ![kopírovat do textarea $B=(0,1), A=[0,1]$](/mathtex/b2/b282444d232e3de2d7fd979b8a729bab.gif) , tak
, tak 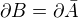 a zaroven
a zaroven  . Do tohoto dokazu by som hranicu netahal.
. Do tohoto dokazu by som hranicu netahal.
Offline
#15 15. 02. 2013 10:32 — Editoval Rumburak (15. 02. 2013 11:41)
Re: uzáver množiny - důkaz
↑ Honza90:
Ahoj. K důkazu té věty potřebuješ použít DVĚ definice.
Definici UZÁVĚRU množiny jsi podal zde ↑ Honza90: , uvědom si ještě definici UZAVŘENÉ MNOŽINY.
Zpravidla se definuje nejprve otevřená množina (což je taková, která s každým svým bodem obsahuje i některé jeho okoli),
uzavřená množina pak je taková, jejímž doplňkem (do celého prostoru) je množina otevřená.
Pojmy otevřenosti a uzavřenosti množin jsou závisle na tom, ve kterém konkretním prostoru jsou míněny.
Tak tedy:
Uzávěr množiny
je množina, ve které má každé epsilonové okolí každého jejího bodu neprázdný průnik s
.
Mějme v prostoru  množinu
množinu  a její uzávěr
a její uzávěr  . Položme
. Položme  a ukažme, že
a ukažme, že  je otevřená v
je otevřená v  .
.
Případ 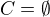 je triviální, nechť dále
je triviální, nechť dále 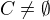 .
.
Předpokládejme, že  NENÍ otevřená v
NENÍ otevřená v  , tedy existuje
, tedy existuje 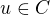 takové, že žádné jeho okolí
takové, že žádné jeho okolí  není částí
není částí  .
.
To znamená (podle definice množiny  ), že v každém takovém
), že v každém takovém  leží některý prvek
leží některý prvek 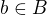 .
.
Některé okolí  takového bodu
takového bodu  je částí
je částí  , protože
, protože 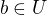 a
a  (jako každé okolí bodu) je otevřená množina.
(jako každé okolí bodu) je otevřená množina.
Ve  nutně existuje některé
nutně existuje některé  , protože
, protože  je okolím bodu
je okolím bodu  , který patří do uzávěru mn.
, který patří do uzávěru mn.  .
.
Máme tedy  takové, že zároveň
takové, že zároveň  .
.
Ukázeli jsme, že existuje 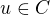 takový, že v každém jeho okolí
takový, že v každém jeho okolí  leží některý prvek množiny
leží některý prvek množiny  , tedy
, tedy 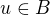 ,
,
takže celkem 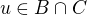 , avšak tento průnik by podle definice množiny
, avšak tento průnik by podle definice množiny  měl být prázdný , což dává spor.
měl být prázdný , což dává spor.
EDIT :
Tím je dokázáno, že  (tedy uzávěr množiny
(tedy uzávěr množiny  ) je uzavřená množina, což je, myslím, ten krok, který Ti nebyl jasný.
) je uzavřená množina, což je, myslím, ten krok, který Ti nebyl jasný.
Viz též ↑ Brano:
Offline
#16 15. 02. 2013 11:14
Re: uzáver množiny - důkaz
↑ Rumburak: Len by som dodal, ze zatial si dokazal, ze uzaver mnoziny je uzavreta mnozina. A este treba ukazat, ze je najmensia - aby si teda ↑ Honza90: nemyslel ze to uz je vsetko. Tu minimalnost ukazal ↑ vlado_bb:.
Offline
#18 15. 02. 2013 14:07
Re: uzáver množiny - důkaz
↑ Rumburak:
to je dobrý důkaz uzavřenosti uzávěru, ale skusím zda to nejde dokázat trochu jednodušeji
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#19 15. 02. 2013 14:33
Re: uzáver množiny - důkaz
Ono vsetko dost zavisi od toho ake definicie pouzivate. Napr. jedna moznost na definovanie otvorenych mnozin je , ze definujes operator uzaveru - co si urobil. Dve z jeho podstatnych vlastnosti su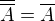
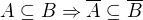
Uzavrete mnoziny na  definujes ako system
definujes ako system 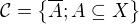 a otvorene ako system
a otvorene ako system 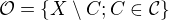 . Pre uzavrete
. Pre uzavrete  lahko dokazes, ze plati
lahko dokazes, ze plati  .
.
Uzavretost uzaveru mas teda rovno z definicie a minimalita je potom jednoducha. Nech  je uzavreta a plati
je uzavreta a plati 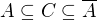 potom
potom 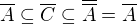 teda
teda 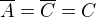 .
.
Predpokladam, ze ste mali ine definicie, ale ak ste to co som pouzil mali dokazane ako vlastnosti, tak to potom mozes pouzit.
Offline
#20 15. 02. 2013 17:12
Re: uzáver množiny - důkaz
↑ Honza90:
Brano použil topologickou definici, kde je to opravdu jednoduché. Ale ani v to metrickém prostoru to není příliš komplikované:
Je-li A uzavřená množina, pak je to triviální, protože 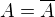 a
a  nemůže platit.
nemůže platit.
Je-li A otevřená, pak  . Jeli
. Jeli  pak existuje
pak existuje  pro který je
pro který je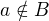 (1)
(1)
Protože  a (1), musí být
a (1), musí být  . Takže pro každé okolí O_a existuje b tak, že
. Takže pro každé okolí O_a existuje b tak, že 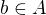 . Protože ale zároveň
. Protože ale zároveň 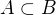 , je také
, je také 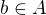 . Znamená to, že a je hraniční prvek B a vzhledem k tomu, že B je uzavřená, musí být
. Znamená to, že a je hraniční prvek B a vzhledem k tomu, že B je uzavřená, musí být 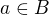 . To je ale spor s (1).
. To je ale spor s (1).
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#21 15. 02. 2013 17:14
Re: uzáver množiny - důkaz
↑ Honza90:
Omlouvám se, zůstal mi tam překlep - předposlední Tex má být  .
.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#23 15. 02. 2013 18:21
Re: uzáver množiny - důkaz
↑ Honza90:
Děkuji, děkuji. Taková maličkost a člověka to potěší :-)
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#24 15. 02. 2013 18:46
Re: uzáver množiny - důkaz
Nechcem nejak extra vyryvat, ale ↑ martisek: tvoj dokaz obsahuje par formalnych chyb.
1) V pripade  uzavretej chceme vylucit "vseobecnejsiu" moznost, kde je iba druha inkluzia vlastna - co samozrejme tiez plati.
uzavretej chceme vylucit "vseobecnejsiu" moznost, kde je iba druha inkluzia vlastna - co samozrejme tiez plati.
2) Mnoziny su aj ine ako otvorene a uzavrete, ale  plati vzdy.
plati vzdy.
Napriek tomu si myslim, ze cela uvaha s hranicou je zbytocna komplikacia. Znova sa jedna iba a dokaz minimality a ten uz urobil ↑ vlado_bb: jednoduchsie.
Offline
#25 15. 02. 2013 19:02
Re: uzáver množiny - důkaz
↑ Brano:
Skutečně pár (tj. dvě) a jsou zcela drobné.
1) to je samozřejmě pravda, ale množna B tak, že  rovněž neexistuje.
rovněž neexistuje.
2) Místo "Je-li A otevřená..." ve druhé části důkazu by mělo být "Není-li A uzavřená" a všechno ostatní může zůstat :-)
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uzáver množiny - důkaz (TOTO TÉMA JE VYŘEŠENÉ)
