Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 02. 2013 15:40
Re: sustava rovnic
↑ Romans1:
z druhé rovnice si vyjádři y a dosaď do první rovnice. Získáš kvadratickou rovnici. Aby rovnice měla reálná řešení, tak diskriminant musí být větší než nula (v tom případě bude mít 2 řešení) nebo roven nule (v tomto případě bude mít 1 reálné řešení).
Offline
#3 17. 02. 2013 15:40 — Editoval ((:-)) (17. 02. 2013 15:42)
Re: sustava rovnic
↑ Romans1:
Dosadíš do prvej rovnice, ktorú potom riešiš pre neznámu x.
Reálne riešenie bude existovať, ak D bude nezáporný...
Offline
#8 17. 02. 2013 16:00 — Editoval ((:-)) (17. 02. 2013 16:01)
Re: sustava rovnic
↑ Romans1:
Myslím, že to máš dobre, alebo máme rovnakú chybu ... :-)
Riešiť pre x...
Ty potrebuješ len diskriminant, tak si ho napíš a polož ho väčší alebo rovný 0...(vtedy bude mať rovnica reálne riešenie).
Offline
#9 17. 02. 2013 16:02 — Editoval mp3jj (17. 02. 2013 16:03) Příspěvek uživatele mp3jj byl skryt uživatelem mp3jj. Důvod: chyba, nebudu už mást :)
#12 17. 02. 2013 16:17 — Editoval ((:-)) (17. 02. 2013 16:18)
Re: sustava rovnic
↑ Romans1:
Vyšlo mi  , teda
, teda  , ale nekontrolovala som nijako... možno overiť 0 by nedalo veľkú námahu...
, ale nekontrolovala som nijako... možno overiť 0 by nedalo veľkú námahu...
Offline
#13 17. 02. 2013 16:23 Příspěvek uživatele Romans1 byl skryt uživatelem Romans1. Důvod: chyba
#15 17. 02. 2013 16:33 — Editoval ((:-)) (17. 02. 2013 16:33)
#17 17. 02. 2013 16:43 — Editoval ((:-)) (17. 02. 2013 16:45)
Re: sustava rovnic
↑ Romans1:
Kvadratická funkcia platí ... :-)
Nevieš ... veď si to riešil, tak ak všetko robíš matematicky správne, nemôžeš mať chybu ...
Dosadila by som pre kontrolu hranice (čísla 2 a -2) a potom ľubovoľné číslo z intervalu -2 až 2.
A ešte aj niečo "mimo" tohto intervalu, "pre istotu" ...
Pre hranice intervalu by mal vyjsť aj hraničný výsledok riešenia rovnice, domnievam sa ...
Offline
#19 17. 02. 2013 16:53
Re: sustava rovnic
↑ Romans1:
2 má byť to c, už som Ti to ukazovala pre nulu ...

 ... toto y máš dosadiť do prvej rovnice
... toto y máš dosadiť do prvej rovnice
Offline
#21 17. 02. 2013 17:23
Re: sustava rovnic
↑ Romans1:
Áno, na hranici je dvojnásobný koreň... (ale -2 som neoverovala)
Offline

 + xy +
+ xy + 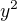 = 1,
= 1,  mozno?)
mozno?)




 toto som dostal..ale.neviem čo s tým:(
toto som dostal..ale.neviem čo s tým:( č
č je výsledok..že?:D
je výsledok..že?:D ... a tak ďalej
... a tak ďalej koreň je 1 to dosadim a vyjde mi ze y je 0 čo sedí...že?:) Dik
koreň je 1 to dosadim a vyjde mi ze y je 0 čo sedí...že?:) Dik