Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 02. 2013 20:47
Slovná úloha - ohraničenosť
Ak pre súčin x,y platí x.y= -38 tak hodnota veličiny 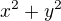 je:
je:
a)ohraničená zhora aj zdola
b)ohraničená zhora a neohraničená zdola
c)neohraničená zhora a ohraničená zdola
d)neohraničená ani zdola ani zhora
...
no je jasné že ked je kladné, tak y musi byt zaporne..a naopak...ale to je ejdno, kedze je to potom vsetko na druhu, vzdy to bude kladne... takže preto zhora by ohraničená byt nemala...lebo možme dat aj napr. 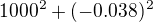 a tak dalej až do nekončečna..
a tak dalej až do nekončečna..
a zdola podla mna je ohraničená..lebo zaporne hodnoty ani len nemoze nadobudat...... takže je podla mna spravna odpoved c
ALE!
nijako sme nevyužili údaj že x.y=-38...
Offline
#2 20. 02. 2013 20:58 — Editoval Arabela (20. 02. 2013 21:05)
Re: Slovná úloha - ohraničenosť
Ahoj ↑ Romans1:,
aj podľa mňa je správna odpoveď c).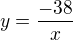 ,
,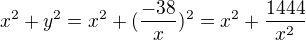 .
.
Ide vlastne o skúmanie vlastností takejto funkcie...
Ty si vo svojich úvahách využil to, že keď je x kladné, y musí byř záporné a tak. V podstate to všetko sedí a konkrétna hodnota -38 by zohrala úlohu možno vtedy, ak by sa nás pýtali na hodnoty miním tej funkcie alebo niečo podobné...
server.gphmi.sk/~domanyov
Offline
#3 20. 02. 2013 21:07 — Editoval Romans1 (20. 02. 2013 21:08)
Re: Slovná úloha - ohraničenosť
↑ Arabela:
preboha, ako ta to napadlo? :O (v tejto otazke, vyjadrujem udiv nad tym, ako ta to napadlo...mylsim tým...ako to,ž e sa na to pozrieš a hned vieš čo a ako?:D)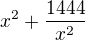
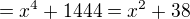
a z tohot urobim kvadraticku rovnicu..čiže...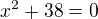 ???? takto sa urobi ta kvadraticka rovnica?
???? takto sa urobi ta kvadraticka rovnica?
inak ak ej to spravne, tak už nemusim robit ani vrchol..už vidim, že zdola ohranicena a zhora nie...spravne?:D
Offline
#4 20. 02. 2013 21:21
Re: Slovná úloha - ohraničenosť
↑ Romans1: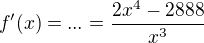

.......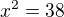
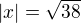
Máme teda dva stacionárne body, teda body, v ktorých je "šanca" na extrém. Pomocou druhej derivácie zistíme, že v oboch prípadoch ide o minimum...
server.gphmi.sk/~domanyov
Offline
#5 20. 02. 2013 21:46
Re: Slovná úloha - ohraničenosť
↑ Arabela:
Prepáč ale vobec ta nechapem...v prvom rade... ako z 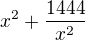 urobit toto
urobit toto 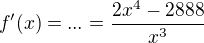 ? :O a ako z toho dostanes
? :O a ako z toho dostanes 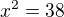 ? :O a ani tie stacionarne body nechapem moc......cize..nechapem vsetko :/ inak ma to byt ucivo do druheho rocnika strednej skoly:D.(ten priklad)
? :O a ani tie stacionarne body nechapem moc......cize..nechapem vsetko :/ inak ma to byt ucivo do druheho rocnika strednej skoly:D.(ten priklad)
Offline
#6 20. 02. 2013 21:57
Re: Slovná úloha - ohraničenosť
↑ Romans1:
To moje riešenie využíva derivácie na hľadanie extrémov.
Ak je to úloha pre druhákov na strednej škole, potom stačia úvahy, ktoré si urobil...
server.gphmi.sk/~domanyov
Offline
#7 20. 02. 2013 23:03 — Editoval Romans1 (20. 02. 2013 23:03)
Re: Slovná úloha - ohraničenosť
↑ Arabela:
hned spokojný:)
inak všeobecne....da sa pvoedat, že trochu ina otzaka, nesuvisiaca s ulohou..
ked mame vyraz 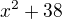 možme z toho urboit kvadraticku rovnicu?
možme z toho urboit kvadraticku rovnicu?
aôebo sa to neda, elbo nevieme comu sa to rovna?
Offline
#8 21. 02. 2013 08:30
Re: Slovná úloha - ohraničenosť
↑ Romans1: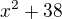 je kvadratický výraz,
je kvadratický výraz,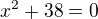 je kvadratická rovnica,
je kvadratická rovnica,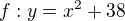 je kvadratická funkcia.
je kvadratická funkcia.
Spolu súvisia, ale neslobodno ich zamieňať.
server.gphmi.sk/~domanyov
Offline
#9 21. 02. 2013 14:21
Re: Slovná úloha - ohraničenosť
↑ Romans1: ↑ Romans1:
Řešení velmi jednoduché, ale derivace na to netřeba. Stačí do jednoho grafu načrtnout funkce  a
a 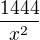 (a vzhledem k otázce se nemusím moc starat o to, aby to bylo zrovna 1444, stačí místo toho jednička) a načrtnout součet (opět stačí velmi zhruba).
(a vzhledem k otázce se nemusím moc starat o to, aby to bylo zrovna 1444, stačí místo toho jednička) a načrtnout součet (opět stačí velmi zhruba).
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline

