Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2013 03:05
Stereometrie pro chytre hlavicky
Nazdarek :) koukala jsem a jste tady vsuchni celkem chytri ;) a doufam proto v odpovedi na dane otazky :) byla bych vam velmi vdecna :) hlavne me zajima postup u danych prikladu :)
1. Odchylka tělesové úhlopříčky kvádru od roviny jeho podstavy je 45°. Určete vztah mezi jeho délkou, šířkou a výškou. (odpověď je c =a
=a +b
+b , přitom a, b, c jsou délka, šířka a výška)
, přitom a, b, c jsou délka, šířka a výška)
2. (už to tady na foru bylo ale spocitali jste to spatne :)) Výška pravidelného čtyřbokého jehlanu ABCDV je rovna délce jeho podstavných hran.Vypočtěte odchylku A) rovin dvou sousedních stěn. (odpověď asi 78°28')
B) protějších stěn (odpověď asi 53°8')
moc diky vsem :)
Offline
#2 26. 02. 2013 07:58 — Editoval Honzc (28. 02. 2013 12:58)
Re: Stereometrie pro chytre hlavicky
↑ ebabuli:
ad1) 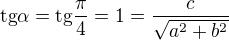
a tedy 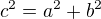
ad2)
Volme počátek souřadné soustavy do středu podstavy jehlanu. (a pro jednoduchost volme stranu rovnou 1)
a)Pak sousední boční stěny mají úsekové rovnice: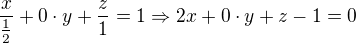
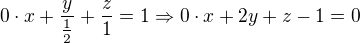
a pro úhel platí:
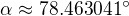
b) 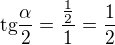
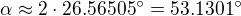
Online
#3 26. 02. 2013 11:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stereometrie pro chytre hlavicky
tady vsuchni celkem chytri
:-) já se nehlásím, jelikož nejsem chytrá, ale jen dobře nacvičena. Pár moderátorských poznámek k úpravě úvodního příspěvku tématu viz pravidla (zejména 2, 3). Pokud jsi našla téma, kde je chyba, je dobré napsat přímo v tématu, ať se opraví. Děkuji.
↑ Honzc:
Zdravím a děkuji (ale nekontrolovala jsem, doufám, že není třeba :-)
Offline
#4 26. 02. 2013 14:53
Re: Stereometrie pro chytre hlavicky
↑ jelena: jo to jo ale to tema uz bylo uzavrene :) http://forum.matweb.cz/viewtopic.php?id=57165
Offline
#6 27. 02. 2013 00:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stereometrie pro chytre hlavicky
↑ ebabuli:
:-) ne, jen označené za vyřešené. Také lze přidat odkaz do nového tématu, co jsi založila, že jsi našla:
(už to tady na foru bylo ale spocitali jste to spatne :))
a přidat svůj dobrý výpočet. Pokud ještě máš nejasno, tak, prosím, do samostatných témat. Děkuji.
Offline
#7 27. 02. 2013 06:25 — Editoval Honzc (06. 01. 2015 13:36)
Re: Stereometrie pro chytre hlavicky
↑ ebabuli:
Úseková rovnice roviny je: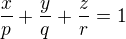
kde  je hodnota, ve které rovina protíná osu
je hodnota, ve které rovina protíná osu 
 je hodnota, ve které rovina protíná osu
je hodnota, ve které rovina protíná osu 
 je hodnota, ve které rovina protíná osu
je hodnota, ve které rovina protíná osu 
Jednu rovinu tvořící stěnu čtyřstěnu ti ukáži:
V mém souřadném systému je jedna přímka roviny rovnoběžná s osou y a osu x protíná v dodě (1/2,0,0) a tedy 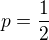
Protože je rovnoběžná s osou y, tak osu y neprotíná a tedy 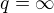 a proto
a proto 
Osu z pak rovina protíná v bodě (0,0,1) a tedy 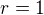
Druhá je obdobná, pouze je rovnoběžná s osou x.
Jinak pokud znáš 3 body ![kopírovat do textarea $M_{k}[x_{x},y_{k},z_{k}]$](/mathtex/03/031952dc6ee30d8a45cb4abf6a192cef.gif) kde
kde 
(neležícími na jedné přímce), kterými rovina prochází pak její rovnici můžeš vypočítat z determinantu
Vyčíslení determinantu (aby to bylo úplně jasné)
Rovnice roviny dané třemi body.![kopírovat do textarea $x[y_{1}(z_{2}-z_{3})+y_{2}(z_{3}-z_{1})+y_{3}(z_{1}-z_{2})]+$](/mathtex/78/780a156f3f36f3eaada2737bde4236e0.gif)
![kopírovat do textarea $y[z_{1}(x_{2}-x_{3})+z_{2}(x_{3}-x_{1})+z_{3}(x_{1}-x_{2})]+$](/mathtex/1a/1a8642b1f66522084e3d16d006eaee78.gif)
![kopírovat do textarea $z[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]-$](/mathtex/72/7221bdef16c7e04394078118c603f039.gif)
![kopírovat do textarea $[x_{1}(y_{2}z_{3}-y_{3}z_{2})+x_{2}(y_{3}z_{1}-y_{1}z_{3})+x_{3}(y_{1}z_{2}-y_{2}z_{1})]=0$](/mathtex/e8/e816208dc860320fb9cbfd9c4d2e7bbb.gif)
Online
#10 06. 03. 2013 12:30
Re: Stereometrie pro chytre hlavicky
↑ Honzc:
Jenom poznámku - je to velice hezké, ale jsme v sekci střední škola. A já už jsem dostal za uši i za to, že jsem tady použil něco tak abstraktního, jako je vektorový součin. Takže s těmi determinanty bych tady byl velmi opatrný :-)
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#11 06. 03. 2013 13:10
Re: Stereometrie pro chytre hlavicky
Ahoj ↑ ebabuli:,
k tej odchýlke protiľahlých stien ihlana ABCDV, napríklad stien BCV a ADV. Označme si ako S1 stred úsečky BC a ako S2 stred úsečky AD. Hľadaná odchýlka protiľahlých stien BCV, ADV je vlastne veľkosťou uhla, ktorý zvierajú úsečky VS1, VS2. ˇˇLahko ho vypočítame z trojuholníka S1S2V napríklad použitím kosínusovej vety.
Najskôr si ale vyjadrime cez Pytagorovu vetu dĺžku bočnej hrany b, pričom vieme, že veľkosť telesovej výšky ihlana je a.
( ).
).
Ďalej si vypočítajme pomocou Pytagorovej vety 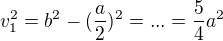
(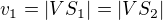 ).
).
Podľa kosínusovej vety platí: ,
,
čo dá po dosadení a úpravách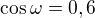
server.gphmi.sk/~domanyov
Offline
#12 06. 03. 2013 14:36
Re: Stereometrie pro chytre hlavicky
Ahoj ↑ ((:-)):,
presne s Tebou súhlasím; je určite jednoduchšie rozdeliť si rovnoramenný trojuholník na dva pravouhlé a počítať polovičný uhol, čo v tomto prípade bolo obzvlášť jednoduché...:)
Mala som na mysli aj túto možnosť, ale uviedla som aj tie medzihodnoty (b, v1), keďže som chcela zareagovať aj na prvú úlohu. Mne totiž vyšiel ten prvý uhol tupý (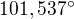 ), čo je doplnkový uhol do
), čo je doplnkový uhol do 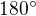 voči výsledku, ktorý uvádza zadávateľka úlohy.
voči výsledku, ktorý uvádza zadávateľka úlohy.
P.S.: Snáď nie je na škodu, že som uviedla spôsob riešenia, ku ktorému by sme sa boli museli uchýliť, keby zadanie nebolo také jednoduché...
A najkrajšie by bolo, keby zadávateľka uviedla ešte nejaké iné, tretie riešenie...:)
server.gphmi.sk/~domanyov
Offline
#13 06. 03. 2013 15:30
Re: Stereometrie pro chytre hlavicky
jste velmi chytri ;) matiku mate v krvi :) uz sem to dokazal propocitat potrebovala jsem radne nakopnout :) a mohla bych pozadat o radu i k odchylka rovin dvou sousedních stěn. (odpověď asi 78°28') hlavne mi dela problem ze ani nevim kde najit uhel, ktery mam vypocitat :-/
Offline
#14 06. 03. 2013 16:01
Re: Stereometrie pro chytre hlavicky
Ahoj ↑ ebabuli:,
najskôr k tomu, čo je odchýlka dvoch rovín. Podľa definície získaš odchýlku dvoch rovín 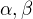 takto: Ľubovoľným bodom
takto: Ľubovoľným bodom  priesečnice
priesečnice  týchto dvoch rovín vedieš rovinu
týchto dvoch rovín vedieš rovinu 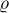 , ktorá je kolmá na zmienenú priesečnicu
, ktorá je kolmá na zmienenú priesečnicu  . Rovina
. Rovina 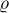 pretne roviny
pretne roviny 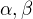 v priamkach
v priamkach 
 . No a uhol priamok
. No a uhol priamok  je súčasne odchýlkou (uhlom) rovín
je súčasne odchýlkou (uhlom) rovín 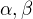 .
.
Znie to jednoducho, ale ako viesť tú pomocnú rovinu 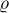 ? A ktorým bodom? A ako získame tie priesečnice
? A ktorým bodom? A ako získame tie priesečnice  ?
?
Našťastie, podľa istého kritéria je rovina kolmá na inú rovinu, ak je kolmá na niektorú priamku tej inej roviny. No a v jednoduchých príkladoch, ako bol práve vyriešený príklad, je voľba pomocnej roviny veľmi jednoduchá - 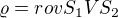 .
.
server.gphmi.sk/~domanyov
Offline
#15 06. 03. 2013 16:21
Re: Stereometrie pro chytre hlavicky
↑ ebabuli:
A teraz k prípadu A) - odchýlka susedných stien.
Budem počítať odvhýlku rovín ABV, BCV.
Ich priesečnica je priamka BV.
Čo bude tým ľubovoľným bodom priesečnice, ktorým vedieme pomocnú rovinu 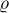 ? (V predošlom prípade B) to bolo jasné - priesečnicu sme nemali znázornenú, mali sme iba jej jediný bod V, ale to nám stačilo...)
? (V predošlom prípade B) to bolo jasné - priesečnicu sme nemali znázornenú, mali sme iba jej jediný bod V, ale to nám stačilo...)
V tomto prípade to však tiež nebude ťažké. Z bodu A veďme kolmicu na BV, jej pätu označme P. Podobne spustime kolmicu z bodu C na BV - dostaneme ten istý bod P. Takže rovina vedená ľubovoľne zvoleným bodom priesečnice kolmona obe roviny bude rovina APC.
Priesečnice s danými rovinami sú priamky AP, PC. Treba zistiť ich uhol.
Pomôžeme si trojuholníkom APC. Je rovnoramenný, so základňou AC,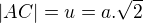 .
.
Označme 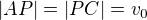 .
.
Vypočítajme dĺžku  z rovnoramenného trojuholníka ABV; napríklad tak, že dvojakým spôsobom vyjadríme obsah trojuholníka ABV:
z rovnoramenného trojuholníka ABV; napríklad tak, že dvojakým spôsobom vyjadríme obsah trojuholníka ABV: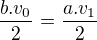 , pričom
, pričom 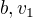 už máme vyjadrené pomocou
už máme vyjadrené pomocou  .
.
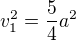
Po jednoduchých úpravách dostaneme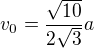 .
.
A teraz môžeme použiť napríklad kosínusovú vetu na trojuholník ACP: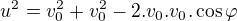 ,
,
a odtiaľ vypočítaš  ...
...
server.gphmi.sk/~domanyov
Offline

