↑ Magee:
Ahoj :),
Začni určením definičního oboru, to by nebylo špatné vědět, když už řešíš nějakou funkci.
- Zprvu vidíme neznámou v čitateli zlomku, tudíž musíme z definičního oboru vyhodit jako možnost nulu (nemůžeme dělit nulou, to je pro nás prostě nechytrá věc a my jsme určitě chytří, že? ;)).
- Další věc co ovlivní definiční obor bude logaritmus. Víme, že argument logaritmu musí být kladný (tj. ne nula, ne záporná čísla) v R.
- Další podmínka už není, protože za x, které je v předpisu samostatné můžeme volit cokoli (tj. R).
- Teď uděláš průnik množin, které ti vyjdou a tí mdostaneš definiční obor (takže D(f) = (0; +oo)).
Když už máme definiční obor, tak se mrkneme na to, jak nám půjde funkce na jeho krajích přes limity (možná zjistíme i nějakou tu asymptotu, co myslíš, vidíš ji nebo tam není?).
Limitu k nule musíme vést zprava, protože logaritmus zleva k nule není (mrkni na graf g(x)=lnx) - ta funkce prostě na levé straně od nuly ani není .)
Limity si vyřeš sama, ok?
Jen snad k těm asymptotám (zatím pouze horizontální a vertikální):
, kde A je nějaké konkrétní vlastní číslo. Pokud limity takto nevyjdou, tak funkce nemá asymptotu vertikální ani horizontální (může vyjít vyklidu jen jedna asymptota a druhá ne, nebo ani jedna, neboj se toho).
Dále omrkni, zda-li je funkce sudá, lichá, periodická.
Perioda: periodu to žádnou nemá, není tam nic co by se mohlo opakovat, to je vidět (ale nějaký důkaz si prověď sama).
Tak co dál? Jasně, zderivujeme funkci a zjistíme, kdy je derivace rovna nule, tím dostaneme body podezřelé z extrému (možné lokální extrémy) a zjistíme, kde je funkce stoupající (první derivace je zde kladná) a kde klesající (první derivace je záporná). Podle toho poznáem i lokální extrémy (maximum/minimum) a určíme jejich souřadnice (prostým dosazováním do funkce).
Poté provedeme druhou derivaci, položíme ji rovnu nule a tím zjistíme inflexní bod(y) (kde se funcke láme z konvexnosti na konkávnost a opačně), podle toho jestli je druhá derivace kladná (konvexní) nebo záporná (konkávní) můžeme určit konvexnost konkávnost (znovu to budou nějaké intervaly). Nezapomeň zjistit souřadnice infelxních bodů, aby se ti lépe kreslilo.
Co teď? Teď bys ještě mohla vyřešit, kde graf funkce protíná (pokud vůbec) osy x,y. Tzn. zjisti toto:
Ještě bych se být tebou pokusil určit obecnou asymptotu, pokud existuje, tak ti to dost ulehčí, takže hledáme přímku ve tvaru y=kx+q a to takto:
Teď už snad můžeme začít kreslit graf funkce. nejprve si zakresli body, které jsi zjistila (extrémy, inflexní body, průsečíky, atp...), asymptoty a pak pokračuj grafem funkce.
Nakonec nezapomeň na důležitou věc a tou je obor hodnot (poznáš z grafu).
Ještě by možná stálo za to, abys určila zda-li je funcke spojitá nebo ne (to si zapiš někam ke kroku sudosti, lichosti,...). Mám to tušení, že tady by ti mohlo stačit, že je funkce spojitá, když je složena ze spojitých funkcí. Vzhledem k tomu, že je složena ze samých elementárních funkcí, o kterých dobře víš, zda-li jsou spojité nebo ne, tak bude hračka to říci o tvé funkci.
Někdo mne určitě poopraví v částech, dke jsem ulétl, já jen doufám, že toho nebylo moc a poslal jsem tě správným směrem
- pro přibližné zakreslení na graf stačí odmocnit a dopočítat přiblížně.
jsou to dvě různé hodnoty, pro přiblížné nakreslení na graf stačí výpočet na kalkulačče.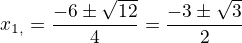
máme celkem 3 podezřelé body – ověřujeme, zda jsou inflexním bodem.
