Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 03. 2013 00:04
opet stereometrie
tak jsem opet narazila na par zadrhelu a nevim co s nimi :( mohl by mi nekdo poradit v ramci strediskolske matematiky nejaky postup :) diky
1) Je dána krychle ABCDEFGH s hranou délky a. Bod P je středem hrany BC, bod Q bodem polopřímky FG tak, že bod G je středem úsečky FQ. bod R leží na polopřímce BF tak, že bod F je středem úsečky BR. Určete vzdálenost bodu ...... od prímky DP
A) bodu Q (vysledek a 14/5)
14/5)
B bodu R (vysledek a 21/5)
21/5)
2) Je dána krychle ABCDEFGH s hranou délky a=4cm, bod M je středem hrany AB a bod N je další bod hrany AB, pro který platí 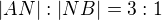 . Určete vzdálenost bodu G od přímky HM. (vylsledek a=osm
. Určete vzdálenost bodu G od přímky HM. (vylsledek a=osm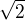 /3)
/3)
Offline
#2 03. 03. 2013 13:42 — Editoval Arabela (03. 03. 2013 13:52)
Re: opet stereometrie
Ahoj ↑ ebabuli:,
k 1.príkladu.
A)
Označme si 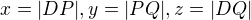 .
.
Aplikovaním Pytagorovej vety ľahko vypočítame ,
,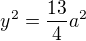 ,
,
(stačilo si uvedomiť, že 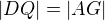 ).
).
Nech  je veľkosť uhla QDP.
je veľkosť uhla QDP.
Podľa kosínusovej vety platí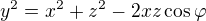 ,
,
odtiaľ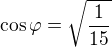 .
.
Ľahko vypočítame  .
.
Uvedomíme si, že vzdialenosť bodu Q od priamky DP je veľkosť výšky z bodu Q v trojuholníku DPQ.
Preto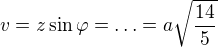 .
.
B) Postupujeme analogicky, ale namiesto trojuholníka DPQ pracujeme s trojuholníkom DPR.
server.gphmi.sk/~domanyov
Offline
