Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vlastní čísla matice a vektorm (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 03. 2013 10:57
vlastní čísla matice a vektorm
Dobrý den,
mám zadání: a(s) je nezáporná reálná fce a mám spočítat vlastní čísla a matice 2x2 matice (0, -1), (a(s)^2,0), dostala jsem se k řešení že  a to myslím že nemá řešení.
a to myslím že nemá řešení.
Pak jsem zkusila prohodit řádky matice (a(s)^2,0), (0, -1) a vyšlo mi že 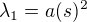 a
a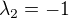 a vlastni vektor pro obě dve čísla je nulový. Lze to vyřešit takto? Nebo to mám špatně? Děkuji
a vlastni vektor pro obě dve čísla je nulový. Lze to vyřešit takto? Nebo to mám špatně? Děkuji
Offline
- (téma jako vyřešené označil(a) simcilka)
#4 19. 03. 2013 15:07
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vlastní čísla matice a vektorm (TOTO TÉMA JE VYŘEŠENÉ)

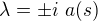 , a vektor mi vychazi že si mohu zvolit za prvni hodnotu jakykoliv parametr, takze (t, -i a(s)t) a druhy (t, i a(s)t), kde t je R, uz je to spravne?
, a vektor mi vychazi že si mohu zvolit za prvni hodnotu jakykoliv parametr, takze (t, -i a(s)t) a druhy (t, i a(s)t), kde t je R, uz je to spravne?