Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 03. 2013 21:58 — Editoval bejf (22. 03. 2013 22:23)
Goniometrická rovnice
Ahoj, nevím si rady s další rovnicí, trochu mě to mate.
Řešte v R rovnici: .
.
Můj postup: si převedu na
si převedu na  , obdobně i
, obdobně i  na
na  a
a  ,
,  taky, takže dostanu:
taky, takže dostanu:
Potom si ty výrazy upravím podle vzorců pro dvojnásobný kořen, ale pak už s tím nemůžu hnout. Děkuji za případné rady.
Offline
- (téma jako vyřešené označil(a) bejf)
#3 22. 03. 2013 22:23
Re: Goniometrická rovnice
↑ martisek:
Jasně ano, samozřejmě jsem udělal chybu tady na fóru. Opravím to. Jinak na papíře počítám tak jak píšeš ty. :-)
Offline
#5 22. 03. 2013 23:23 — Editoval bejf (22. 03. 2013 23:24)
Re: Goniometrická rovnice
↑ zdenek1:
Myslel jsem si, že bych se k tomu nějak mohl dostat přes sinx a cosx. Tvůj postup mě nenapadl a ani ho popravdě celkem moc nechápu.
Rozuměl bych tomu, jak jsi došel na  na levé straně, ale už mi uniká jak jsi došel k té pravé straně.
na levé straně, ale už mi uniká jak jsi došel k té pravé straně.
A výsledek by měl být  . Tak právě už vůbec nějak nevím.
. Tak právě už vůbec nějak nevím.
Offline
#6 22. 03. 2013 23:39
Re: Goniometrická rovnice
↑ bejf:
K pravé straně dojdeš úplně stejně jako k levé: 
 je dobře.
je dobře.
Z toho mého ho dostaneš, když vyloučíš podmínky (což jsem udělal v a), v b) už jsem to nepsal, ale udělat se to samozřejmě musí)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 23. 03. 2013 08:14
Re: Goniometrická rovnice
↑ zdenek1:
Opravdu se omlouvám, ale stále nechápu tu pravou stranu. Asi se moje představa liší od tvého postupu.
Já si představil na levé straně  .
.
Což ale na pravé straně nejde. Takže asi postupuju špatně.
Offline
#9 23. 03. 2013 11:43
Re: Goniometrická rovnice
↑ zdenek1:
Aha, no tak to mě mohlo napadnout no. Podmínky mi jsou jasné, ikdyž mi to dalo trochu práce. No ale dobré vědět, a moc děkuji za vysvětlení a za trpělivost. :-)
Offline







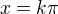 není řešení (podmínky)
není řešení (podmínky)





