Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jak dokázat, že relace X | y je antisymetrická.
#1 31. 03. 2013 11:07
- dendulka1991

- Zelenáč
- Příspěvky: 19
- Škola: gymnázium
- Pozice: student
- Reputace: 0
Jak dokázat, že relace X | y je antisymetrická.
Ahoj, obracím se se na vás s dotazem. Jak mohu jednoduše dokázat, že relace x | y je na množině ℤ antisymetrická. Tranzitivnost a reflexivitu jsem dokázala hravě, ale s tímto si marně lámu hlavu. Děkuji moc!
Offline
#2 31. 03. 2013 11:46 Příspěvek uživatele Honza90 byl skryt uživatelem Honza90. Důvod: špatná odpověď
#3 31. 03. 2013 11:48 — Editoval jarrro (31. 03. 2013 11:54)
Re: Jak dokázat, že relace X | y je antisymetrická.
ak súčasne
tak existujú celé čísla
také, že platí
potom
teda aj
keby platilo
tak by bolo
teda 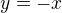
príklad 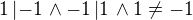
teda nie je antisymetrická vyššie je ukázané , že antisymetria sa môže porušiť len znamienkom
ak ide len o nezáporné čísla tak to samozrejme antisymetrické je, lebo potom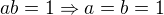
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jak dokázat, že relace X | y je antisymetrická.
