Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 04. 2013 12:57
Přijímačky na VŠ
Nemohl byste mi prosím někdo poradit, jak vyřešit následující dva příklady:
1) Zvětší-li se počet prvků o jeden, zvětší se počet variací třetí třídy z nich vytvořených bez opakování o 126. Určete počet prvků.
2) Rovnice kružnice opsané trojúhelníku, jehož vrcholy jsou body A=![kopírovat do textarea $[4,4]$](/mathtex/c0/c01846a65d11c029d9720162f5bf2274.gif) ; B=
; B=![kopírovat do textarea $[2,-4]$](/mathtex/08/0878dd8963bf3a2232bee1dd551aa8ad.gif) ; C=
; C=![kopírovat do textarea $[-1,-1]$](/mathtex/73/73fe4b05ac44cbe15f7af8d4556e5f81.gif) , lze napsat ve tvaru:??
, lze napsat ve tvaru:??
Mnohokrát děkuji.
Offline
- (téma jako vyřešené označil(a) jelena)
#7 04. 04. 2013 14:09 — Editoval Cheop (04. 04. 2013 14:31)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Přijímačky na VŠ
↑ luuu:
Tady v tom případě je to jednoduché
Protože vektory AC a BC jsou na sebe kolmé (jejich skalární součin je 0)
jedná se o pravoúhlý trojúhelník a pro střed kružnice opsané platí, že je ve středu přepony a poloměr je 1/2 přepony.
Napsat rovnici kružnice pokud známe souřadnice středu a její poloměr už není tak těžké.
Mělo by ti vyjít: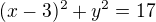
Nikdo není dokonalý
Offline
#9 04. 04. 2013 14:15 Příspěvek uživatele Cheop byl skryt uživatelem Cheop.
#10 04. 04. 2013 14:22 Příspěvek uživatele marnes byl skryt uživatelem marnes.
#11 04. 04. 2013 14:23 — Editoval Cheop (04. 04. 2013 14:28) Příspěvek uživatele Cheop byl skryt uživatelem Cheop.
#14 08. 04. 2013 12:06 — Editoval luuu (08. 04. 2013 12:08)
Re: Přijímačky na VŠ
Děkuju :)
Narazila jsem ještě na další příklady, kterým nerozumím a to:
1) Poloměr kružnice 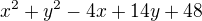 =0 je roven číslu ?? (správná odpověď
=0 je roven číslu ?? (správná odpověď  )
)
2) Počet všech  ,pro která platí
,pro která platí 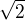 sinx + sin2x=0, je roven číslu ??? (správná odpověď 5)
sinx + sin2x=0, je roven číslu ??? (správná odpověď 5)
3) Obecnou rovnici přímky, která prochází středem kružnice 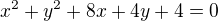 a je kolmá na vektor (-2,r), kde r je poloměr kružnice, lze napsat ve tvaru??? (x-2y=0)
a je kolmá na vektor (-2,r), kde r je poloměr kružnice, lze napsat ve tvaru??? (x-2y=0)
Jsem vám nade vše zavázána za vaši pomoc!
Offline
#15 08. 04. 2013 12:43 — Editoval Cheop (08. 04. 2013 12:45)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Přijímačky na VŠ
↑ luuu:
Př. 3)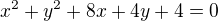 - převedeme na středový tvar:
- převedeme na středový tvar: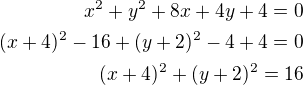
Poloměr je: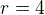
Střed: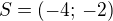
Vektor je: = normálový vektor hledané přímky (jistě víš proč)
= normálový vektor hledané přímky (jistě víš proč)
Rovnice přímky dosazením souřadnic středu kružnice dopočteme c tj:
dosazením souřadnic středu kružnice dopočteme c tj:
Rovnice přímky: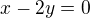
Nikdo není dokonalý
Offline
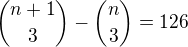

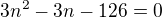

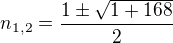
 - nevyhovuje
- nevyhovuje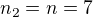 - výsledek
- výsledek
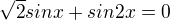
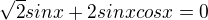
 součin je roven nule, když jeden z výrazů je roven nule, takže rozdělíme na 2 situace
součin je roven nule, když jeden z výrazů je roven nule, takže rozdělíme na 2 situace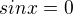 a
a 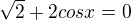
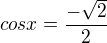 a dořešíš v zadaném intervalu
a dořešíš v zadaném intervalu je výraz
je výraz  roven...
roven... , pro která platí
, pro která platí ![kopírovat do textarea $\sqrt[]{3}cos x + sin (2x) = 0$](/mathtex/91/917cf7ac5f89bc6da914896945e26ff7.gif) , je roven číslu...
, je roven číslu...![kopírovat do textarea $A=[3,-4] , B= [2,-1], C= [-1,-2]$](/mathtex/c7/c7cf7cb88bbdbeb8279d9c5dabf498ac.gif) . Obecnou rovnici přímky, v níž leží těžnice Tc, lze napsat ve tvaru...
. Obecnou rovnici přímky, v níž leží těžnice Tc, lze napsat ve tvaru...
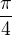 je to samé jako
je to samé jako 
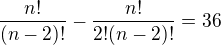 - úpravou:
- úpravou:
