Matematické Fórum

jelinekgreen · 14. 04. 2013 20:46

Zdravím, mohl by mi někdo prosím napsat postup, jak vyřešit tento integrál? Postup vím. Typových příkladů jsem počítal už tucet a všechny mi vyšly, až na tento. Výsledek je ověřen strojem, takže chyba ve výsledcích není. Počítal jsem ho už 5x a furt mi vychází stejně blbě. Asi jsem zablokovanej... Resp. jednou mi vyšel, ale po bujarých oslavách jsem našel chybu ve výpočtu, takže nic.

Tady je ten rošťák: 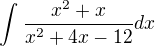$\int_{}^{} \frac{x^{2}+x}{x^{2}+4x-12}dx$

Můj opakovaný výsledek: 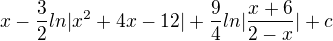$x-\frac{3}{2}ln|x^{2}+4x-12|+\frac{9}{4}ln|\frac{x+6}{2-x}|+c$

A tohle je správný výsledek: 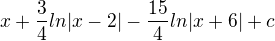$x+\frac{3}{4}ln|x-2|-\frac{15}{4}ln|x+6|+c$

Byl bych hrozně rád, kdyby mi někdo pomohl... Předem moc děkuji ;)

standyk · 14. 04. 2013 20:56

↑ jelinekgreen:

Ahoj,
pomocou základných vlastností logaritmu sa ten Tvoj výsledok dá upraviť na ten ktorý máš v knihe
$x-\frac{3}{2}\ln|x^{2}+4x-12|+\frac{9}{4}\ln|\frac{x+6}{2-x}|+c =\nl =x-\frac{3}{2}\ln|(x-2)\cdot(x+6)|+\frac{9}{4}\ln|{\frac{x+6}{2-x}}|+c =\nl =x-\frac{3}{2}\ln|x-2|-\frac32|x+6|+\frac{9}{4}\ln|x+6|-\frac94\ln|2-x|+c =\nl =x+\frac{3}{4}ln|x-2|-\frac{15}{4}ln|x+6|+c$

Čiže z toho vyplýva že Tvoj výsledok je správny :)

jelinekgreen · 15. 04. 2013 10:13

↑ standyk: Díky, ačkoli mě to vlastně nepotěšilo :D

Ale pořád v tom trochu plavu, ten poslední krok nemůžu dát správně dohromady. Lítaj mi tam znamínka. Nechtěl bys mi to prosím rozepsat úplně polopatě?

Děkuju...

standyk · 15. 04. 2013 15:39

↑ jelinekgreen:

tam keďže máš absolútnu hodnotu tak môžeš urobiť toto:
$=x-\frac{3}{2}\ln|x-2|-\frac32\ln|x+6|+\frac{9}{4}\ln|x+6|-\frac94\ln|\color{red}{2-x}\color{black}|+c =\nl =x-\frac{3}{2}\ln|x-2|-\frac32\ln|x+6|+\frac{9}{4}\ln|x+6|-\frac94\ln|\color{red}{x-2}\color{black}|+c =\nl =x+\frac{3}{4}\ln|x-2|-\frac{15}{4}\ln|x+6|+c$
a potom ščítaš čo je spoločné.

jelinekgreen · 15. 04. 2013 21:02

↑ standyk:

No, mně to stejně podle tohoto schématu nevychází. Mně těch 15/4 vychází na (x-2) a opačně. Každopádně jsem to ještě jednou přepočítal a objevil jsem jedno skryté znaménko, resp. závorku a vyšlo mi to, takže jsem se dopracoval.

Zaráží mě ale jiná věc. Jak online kalkulačka, tak spolužák, k těm zlomkům dospěli velmi rychle, hned z kraje výpočtu. Já až po dlouhých úpravách. Jaký je jiný postup, dostat se k výsledku rychleji?

Každopádně moc děkuju :))

Matematické Fórum

#1 14. 04. 2013 20:46

Integrál - parciální zlomky

#2 14. 04. 2013 20:56

Re: Integrál - parciální zlomky

#3 15. 04. 2013 10:13

Re: Integrál - parciální zlomky

#4 15. 04. 2013 15:39

Re: Integrál - parciální zlomky

#5 15. 04. 2013 21:02

Re: Integrál - parciální zlomky

Zápatí