Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 24. 04. 2013 20:50
Re: logaritmická rovnice
↑ Aktivní:
No ona nie je nutná, ale v princípe to pomocou nej je "viac vidieť".
1^6 - 2^6 + 3^6 = 666
Offline
#5 24. 04. 2013 21:02 — Editoval 010010 (24. 04. 2013 21:16)
- 010010

- Příspěvky: 82
Re: logaritmická rovnice
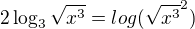
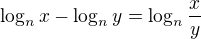
![kopírovat do textarea $-2\log_{3}(x\sqrt[3]{x})=-\log_{3}((x\sqrt[3]{x})^2)$](/mathtex/3c/3c8cb304ea91ed02b29eac4f169ff56e.gif) alebo
alebo ![kopírovat do textarea $-2\log_{3}(x\sqrt[3]{x})=\log_{3}\frac{1}{(x\sqrt[3]{x})^2}$](/mathtex/73/738d3ec12c0a21d6c1d8a80063d4c53c.gif)
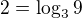
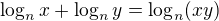
Takže:
Si to môžeme celé prepísať.![kopírovat do textarea $
\log_{3}x^3 + \log_{3}\frac{1}{\sqrt[3]{x}}+ \log_{3}x + \log_{3}\frac{1}{x^2\sqrt[3]{x^2}}= \log_{3}x + \log_{3}\frac{1}{x}$](/mathtex/60/60b881c37aa8b15a11f08d293f890042.gif)
postupne máme ![kopírovat do textarea $\log_{3}(\frac{x^3x}{\sqrt[3]{x}x^2\sqrt[3]{x^2}})=\log_{3}\frac{9}{x}$](/mathtex/eb/ebf541e38ccb69351c980c0bd374724f.gif)
teda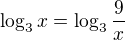 "od-logaritmujeme", a máme
"od-logaritmujeme", a máme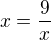
A potom počítame kvadratickú rovnicu.
Offline
![kopírovat do textarea $2log_{3}\sqrt{x^{3}}-log_{3}\sqrt[3]{x}+log_{3}x-2log_{3}(x\sqrt[3]{x})=2-log_{3}x$](/mathtex/eb/eb7dd7c2e882279a3a101c11d07a06b8.gif)
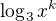 a použi to, že
a použi to, že 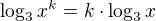 a substitúcia
a substitúcia 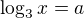
![kopírovat do textarea $\sqrt[a]{b^{c}}=b^{\frac{c}{a}}$](/mathtex/66/66a3797dea7a6f134671b383b56766a6.gif)