Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 04. 2013 19:54
- blanička.č.
- Příspěvky: 31
- Reputace: 0
logaritmy
dobry den potebovala bych poradit s temito priklady - nevím co s těmi odmocninami
- nevím co s těmi odmocninami - mám použít substituci, ze které jsem dostala že y1=5 a y2=-2, ale nevím jak to upravit dál
- mám použít substituci, ze které jsem dostala že y1=5 a y2=-2, ale nevím jak to upravit dál - opět mám použít substituci, ale vůbec mi tenhle příklad nevychízí
- opět mám použít substituci, ale vůbec mi tenhle příklad nevychízí
Děkuji
Offline
- (téma jako vyřešené označil(a) marnes)
#2 28. 04. 2013 20:14 — Editoval ado130 (28. 04. 2013 20:21)
Re: logaritmy
2. príklade už len dosadíš do tej substitúcie, čiže 

Čiže budeš mať 2 výsledky.
Ten 3. príklad máš jednoduchý.
Miesto  si zaveď napr.
si zaveď napr.  , vznikne ti kvadratická rovnica, výsledok bude iba 1. Následne sa vrátiš späť, takže budeš mať niečo takéto
, vznikne ti kvadratická rovnica, výsledok bude iba 1. Následne sa vrátiš späť, takže budeš mať niečo takéto  a to už budeš určite vedieť dopočítať.
a to už budeš určite vedieť dopočítať.
Quidquid latine dictum sit, altum videtur.
Offline
#3 28. 04. 2013 20:30
- blanička.č.
- Příspěvky: 31
- Reputace: 0
Re: logaritmy
↑ ado130:
u kvadratické rovnice která je y na druhou-2y+1 mi vychází diskriminant 8
Offline
#4 28. 04. 2013 21:15
Re: logaritmy
↑ blanička.č.:
1)







Umocňování není ekvivalentní úprava,  je falešný kořen a rovnici vyhovuje jen pětka.
je falešný kořen a rovnici vyhovuje jen pětka.
2)
Substituce  a řešíme kvadratickou rovnici.
a řešíme kvadratickou rovnici.

Návrat k substituci:

3)
Substituce 



Návrat k substituci:
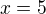
Offline
#6 28. 04. 2013 21:29
#7 29. 04. 2013 10:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: logaritmy
↑ bejf:
zda rozumí, jak se opisuje hotové řešení - bez pochyby :-) V případě řešení od SŠ kolegů mi ani tak nevadí, když napíšete řešení komplet (naopak - cvičíte na tom a dá se pozorovat vývoj a výcvik odborné základny). Děkuji za podrobné řešení, jen doplním, že chybí poznámka o podmínkách (u log. rovnic podstatné).
Ovšem také je dobré se věnovat a analyzovat sdělení autorů dotazů: co naznačuje toto sdělení?
blanička.č. napsal(a):
u kvadratické rovnice která je y na druhou-2y+1 mi vychází diskriminant 8
Děkuji, zdravím.
Offline
#8 25. 01. 2014 14:59 Příspěvek uživatele Gabrielova byl skryt uživatelem Gabrielova.
#9 25. 01. 2014 15:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: logaritmy
↑ Gabrielova:
Zdravím, založ si, prosím, vlastní téma viz pravidla. Tato úloha zde již byla konzultována, zkus projít sekci SŠ za poslední období. Děkuji.
Offline
#10 24. 09. 2015 21:46
Re: logaritmy
Ahoj potřebovala bych poradit jak vypočítat tento příklad. Mám zadány 2 logaritmy : log 2 = 0,301030 a log 5 = 0,69897 a mám určit bez kalkulátoru log 80. Prosím o vysvětlení postupu jak dané logaritmy spočítat aby mi vyšel log 80. Předem moc děkuji !
Offline
#17 24. 09. 2015 22:08 — Editoval marnes (24. 09. 2015 22:09)
- marnes

- Příspěvky: 11227
Re: logaritmy




 a zbytek je práce kalkulačky
a zbytek je práce kalkulačky
Jo. A na začátku vás zdravím.
Offline
#18 24. 09. 2015 22:14
Re: logaritmy
↑ marnes:
Jé děkuji moc a jsem ráda za vysvětlení alespoň pak vím postup a mohu řešit podobné příklady. Mohu ještě naposledy poprosit o tento typ příkladu ? : ((1,06)^n -1)/0,06=20 a (1-(1,025)^-n)/0,025=3 nevím pak jak přehazovat na jednotlivé strany a jak vypadá daný postup, tak budu opět moc vděčná a už je to poslední problém :)
Offline
#24 24. 09. 2015 23:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: logaritmy
Zdravím,
↑ licr: podle pravidel si, prosím, zakládej vždy nové téma na nový dotaz, nepiš do cizích a již vyřešených - viz pravidla a také to povídám zrovna o příspěvek výš, než ten Tvůj ↑ příspěvek 9:. Děkuji.
Offline



 a to už umíš
a to už umíš


 a to už umíš
a to už umíš