Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednoduchý integrál - chyba ve znaménku (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 04. 2013 22:30
Jednoduchý integrál - chyba ve znaménku
Vyřešil jsem tento integrál: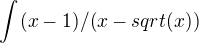
a to tímto způsobem: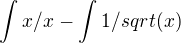
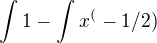
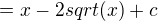
Jenže ve výsledcích (i na wolframu, který na řešení používá substituci) je to takto: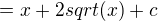
Zkoušel jsem to několikrát a vždy mi vyšlo mínus. Tak by mě zajímalo jak byste to řešili nebo kde by jste hledali chybu. Díky.
Offline
- (téma jako vyřešené označil(a) Firejs)
#4 29. 04. 2013 23:16
- 010010

- Příspěvky: 82
Re: Jednoduchý integrál - chyba ve znaménku
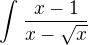
substitúcia: 
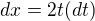
Takže: 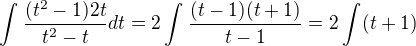
dopočítať dúfam už vieš
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednoduchý integrál - chyba ve znaménku (TOTO TÉMA JE VYŘEŠENÉ)
 .
.