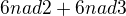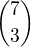Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 01. 05. 2013 23:27
Re: Kombinační číslo
↑ wolfito:
To já taky ne, už jenom z toho důvodu, že můžeš najít víc kombinačních čísel, jejichž hodnota je 35.
Spíš použij pravidlo .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#5 02. 05. 2013 01:11 — Editoval hradecek (02. 05. 2013 01:16)
Re: Kombinační číslo
↑ wolfito:
A ak by si si "náhodou" nemohol na ten vzorec spomenúť, tak to ide aj úpravami:
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline