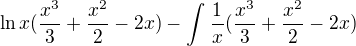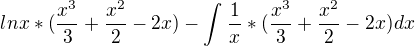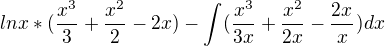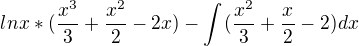Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 05. 2013 20:54
Per partes
Pěkný večer.
Mám vypočitaný příklad a nevím, zda je správně vypočten.
Dáno: 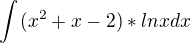


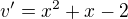
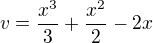
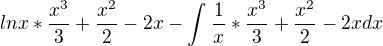
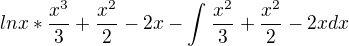

Je to možné ?
Lámu si s tím hlavu a jestli to bude dobře, tak by to šlo určitě ještě mezi sebou vynásobit..
Prosím za radu a předem moc a moc děkuji
Kajman
Offline
- (téma jako vyřešené označil(a) kajman)
#8 05. 05. 2013 21:40
- 010010

- Příspěvky: 82
Re: Per partes
ano, až na ten integrál. Ten tam už nieje pretože si už integrovala :)
Offline