Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 05. 2013 10:32
Lineární algebra - vektorový prostor
Zdravím,
potřeboval bych poradit s tímto příkladem. Zde mám spíš potíž, že ty vektory mají maticové souřadnice:
Ukažte, že prvky tvoří bázi prostoru  . Ukažte, že prvek
. Ukažte, že prvek 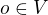 a určete ô souřadnice prvku
a určete ô souřadnice prvku 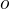 v této bázi. (Místo
v této bázi. (Místo 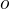 má být
má být  , ale nepodařilo se mi udělat vakoň nad z.)
, ale nepodařilo se mi udělat vakoň nad z.)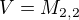
![kopírovat do textarea $A_{1}= [\frac{1,4}{1,0}]$](/mathtex/59/596df07162f949ccc4cbf2bd75c60176.gif)
![kopírovat do textarea $A_{2}= [\frac{2,-2}{0,3}]$](/mathtex/ea/ea50441654c9818ca8e0c39ecc0cf976.gif)
![kopírovat do textarea $A_{3}= [\frac{2,0}{-1,5}]$](/mathtex/d8/d84c51ccf875892f36aa25072ac9e5d6.gif)
![kopírovat do textarea $A_{4}= [\frac{0,4}{1,-3}]$](/mathtex/af/af67b818496acffa2fb35a19576bad63.gif)
![kopírovat do textarea $o= [\frac{5,6}{1,5}]$](/mathtex/1c/1c57bc008c44f795e2678c51cc507d56.gif)
(Byl jsem trochu kreativní, tak si to představte jako matici)
Děkuji za pomoc! :)
Offline

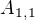 ,
, 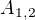 ,
, 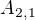 ,
, 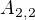 ) jako kdyby to byl normalni vektorovej prostor R4 a pak to prevedes zpatky na prostor matic
) jako kdyby to byl normalni vektorovej prostor R4 a pak to prevedes zpatky na prostor matic![kopírovat do textarea $A_{1,1} =[1,2,2,0]$](/mathtex/3a/3a3802b22c9565a680f5bf577b52341d.gif)
![kopírovat do textarea $A_{1,2} =[4,-2,0,4]$](/mathtex/89/8913a2e3c33c9ec5e084985d3b17596f.gif)
![kopírovat do textarea $A_{2,1} =[1,0,-1,5]$](/mathtex/f6/f63adf6e4e5ce1da5f0c67b90dbb14d3.gif)
![kopírovat do textarea $A_{2,2} =[0,3,5,-3]$](/mathtex/a4/a4b0ee6ae062655ddd97f3620501b7d5.gif)
 sou slozky tech matic, takze ty vektory budou
sou slozky tech matic, takze ty vektory budou