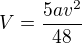Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 05. 2013 19:05
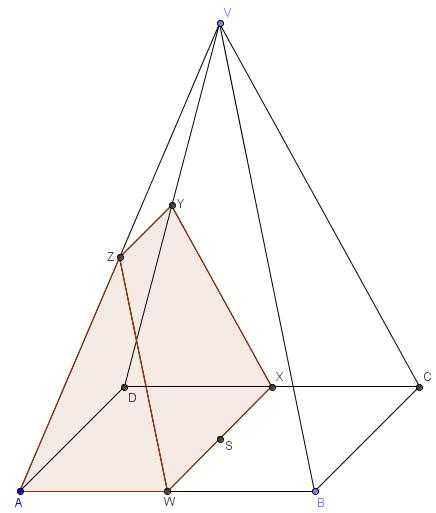
Re: Objem tělesa
↑ Keeeeke:
místo a.v^2 bude určitě a^2.v. A mně vychází 7/32.a^2.v
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#3 28. 05. 2013 19:31
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Objem tělesa
Cau,
pekna uloha. Ja teda souhlasim, ze to bude  .
.
Libi se mi, ze vysledek nezalezi na presne poloze bodu V a ze cele pocitani se da delat pekne (tj. z hlavy).
Offline
#6 28. 05. 2013 21:33
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Objem tělesa
↑ Freedy:
Ja jsem si to rozdelil na jehlan AWXDZ a ctyrsten (tedy taky jehlan) DXYZ.
Objem jehlanu AWXDZ je ctvrtina objemu celeho jehlanu (ABCDV), protoze podstava je polovicniho obsahu a vyska je taky polovicni oproti celemu jehlanu.
Objem jehlanu DXYZ je sestnactina objemu celeho jehlanu. To pocitam tak, ze se na nej divam jako na jehlan s podstavou DXY a vrcholem Z. Zacnu s jehlanem DCVA (ten ma polovicni objem oproti celemu jehlanu), pak bod A priblizim na polovinu k rovine DCV, cimz dostanu jehlan DCVZ s polovicnim objemem nez DCVA. Nakonec jehlanu DCVZ ctyrikrat zmensim obsah podstavy, cimz dostanu jehlan DXYZ.
Offline