Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 01. 2009 19:21
- marnes

- Příspěvky: 11227
Neurčitý integrál
Integrál ze zlomku. V čitateli tři krát x na druhou mínus 4, ve jmenovateli pět krát x na třetí plus 2. Naťukne mně někdo?
Jo. A na začátku vás zdravím.
Offline
#2 20. 01. 2009 22:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál
Zdravím :-)
Je zadání dobře? - pokud ho zadám zde: http://wims.unice.fr/wims/wims.cgi nebo zde: http://user.mendelu.cz/marik/maw/index. … m=integral , tak nevypadné nic hezkého
Je také pro Přerov?
Offline
#6 21. 01. 2009 09:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál
↑ marnes:
přes parciální zlomky to asi půjde (výraz v jmenovateli - vytknout 5 a rozložit podle (a^3 +b^3) - reálný a komplexný kořeny, ovšem nezávidím práci s třetí odmocninou z (2/5), ale to bude moji lenosti :-)
Offline
#7 21. 01. 2009 10:01
Re: Neurčitý integrál
Je to opravdu tak tezke? Kdyz to rozdelim na soucet, tak prvni cast povede na nejaky logaritmus, jak pise ↑ Chrpa:, a druha cast (po vytknuti vhodne konstanty) da  . Tady treba substituce
. Tady treba substituce ![kopírovat do textarea $x=\sqrt[3]ay$](/mathtex/8e/8ec5f67b566d65fdc1bcedce2ce91325.gif) a zase nejake vytknuti konstanty da
a zase nejake vytknuti konstanty da  , no a protoze
, no a protoze  je dale nerozlozitelne v
je dale nerozlozitelne v 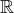 , mame jednoduchy parcialni zlomek.
, mame jednoduchy parcialni zlomek.
Offline
#8 21. 01. 2009 10:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Neurčitý integrál
↑ musixx:
Zdravím :-)
já jsem neřekla "těžké", ale "nehezké" a "práce s 3. odmocnicnou z 2/5...", jinak návrh postupu mám shodný, ale jsem velmí liný estet :-)
Offline
#9 21. 01. 2009 10:48
Re: Neurčitý integrál
↑ jelena: Taktéž zdravím. :-)
No vždyť já jsem také neřekl, žes to vlastně nevyřešila, jen jsem chtěl ukázat, jak je třeba možno si tu "škaredou odmocninu" na chvilku odložit třeba pomocí té substituce, i když -- jak už jsem někde tady v té integrální vlně, která se tady posední týden strhla, napsal -- lineární substituce nijak nepřispěje ke zjednodušení řešení, maximálně jej vizuálně zpřehlední.
Offline
#11 21. 01. 2009 12:05
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Neurčitý integrál
↑ kotry:podivejte se na integralni stredni hodnotu
Offline
 pak by substituce byla pěkná
pak by substituce byla pěkná