Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 21. 01. 2009 15:50
Re: nekonečná řada
↑ Crovn:
Vyšlo ti to opačne. A=1, B=-1. Teraz už len vypisuj členy: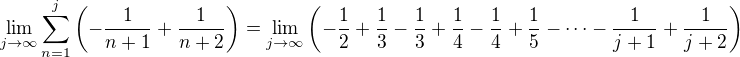
Odtiaľ môžeš vidieť, že susedné členy sa postupne vysčítajú a ostane: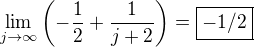
Teda súčet je záporná jedna polovica.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline