Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 06. 2013 22:32
limita integrálu
Dobrý den, chtěla zdali řeším správně tento integrál, popř radu o postup se substitucí, jelikož se nerada učím vzorce nazpamět. jsem si rozdělila na 2 integrály
jsem si rozdělila na 2 integrály 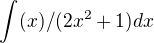 což je
což je 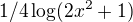 a
a 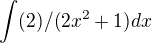 coz mi vyslo
coz mi vyslo a tento ingrál jsem řešila podle vzorce
a tento ingrál jsem řešila podle vzorce 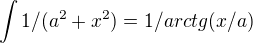 ale nevim jak se na tento vzorec prišlo. Mám dále spočítat
ale nevim jak se na tento vzorec prišlo. Mám dále spočítat  a tady jsem zapomněla jak je s tou větou. Prosím mohl byste mi to někdo dovysvětlit
a tady jsem zapomněla jak je s tou větou. Prosím mohl byste mi to někdo dovysvětlit
Offline
- (téma jako vyřešené označil(a) simcilka)
#5 02. 06. 2013 15:59
Re: limita integrálu
↑ Brano:
omlouvam se nedopsala jsem cely reseni prikladu, ta funkce byla oznacena 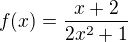 mela jsem spocitat integral a pak nasledne tu limitu, tedy kdyz jsem provedla záměnu integrálu a limity dostanu vysledek nekonecno je to spravne? A kdyz tedy budu mít spočítat
mela jsem spocitat integral a pak nasledne tu limitu, tedy kdyz jsem provedla záměnu integrálu a limity dostanu vysledek nekonecno je to spravne? A kdyz tedy budu mít spočítat  tak to provedu jak?
tak to provedu jak?
Offline

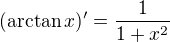
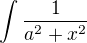
 pred zatvorku a substituuj
pred zatvorku a substituuj 
 je vhodne slusna tak
je vhodne slusna tak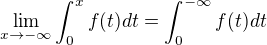
 a integruje sa voci
a integruje sa voci  a este k tomu je
a este k tomu je