Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hanh-Banachova věta v normovaném tvaru - důkaz
#1 02. 06. 2013 20:58
Hanh-Banachova věta v normovaném tvaru - důkaz
Ahoj, mám větu: Nechť X je reálný normovaný prostor a 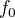 je lineární ohraničený funkcionál definovaný v lineární varietě
je lineární ohraničený funkcionál definovaný v lineární varietě 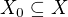 . Pak existuje lineární ohraničený funkcionál f definovaný v X tak, že f(x) = f0(x) pro
. Pak existuje lineární ohraničený funkcionál f definovaný v X tak, že f(x) = f0(x) pro  a platí
a platí 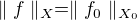 .
.
No a v důkazu pak hnedka na začátku položím 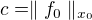 a pak definuji funkcionál
a pak definuji funkcionál  No a dál by mělo být zřejmý, že funkcionál je konečný a konvexní. Konvexní chápu, ale kde se bere konečný?
No a dál by mělo být zřejmý, že funkcionál je konečný a konvexní. Konvexní chápu, ale kde se bere konečný?
Offline
#2 03. 06. 2013 10:37 — Editoval Rumburak (03. 06. 2013 10:50)
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
Ahoj.
Ten termín "ohraničený" lineární funkcionál je nutno vnímat v tom smyslu, že má pouze konečnou normu,
tedy nikoliv, že by byla ohraničená možina jeho funkčních hodnot (protože v takovém případě by jediným
ohraničeným l.f. byl funkcionál identicky rovný nule). Tvůj problém by mohl plynout z nesprávného
pochopení této definice.
"Konečný" funkcionál je podle mne každý, který nabývá pouze konečných hodnot, ať již je ohraničený
nebo ne. Je též možné, že je slovo "konečný" v důkaze použito omylem místo "ohraničený" .
Musel bych ten důkaz vidět celý, abych mohl odpovědět vyčerpávajícím způsobem.
Offline
#3 03. 06. 2013 11:32
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Rumburak: celý důkaz je tady: 
vztah 3.13 je toto: 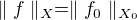
věta 3.13 je Hahn-Banachova věta: Nechť X je reálný lineární prostor a  je jeho podprostor. Nechť dále p je konečný konvexní funkcionál v X a
je jeho podprostor. Nechť dále p je konečný konvexní funkcionál v X a 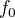 je lineární funkcionál v
je lineární funkcionál v  , přičemž
, přičemž  . Pak existuje lineární funkcionál f definovaný v X, který je prodloužením funkcionálu
. Pak existuje lineární funkcionál f definovaný v X, který je prodloužením funkcionálu 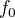 a který splňuje nerovnost
a který splňuje nerovnost 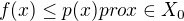 .
.
vztah 3.5: 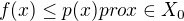
Offline
#4 03. 06. 2013 11:55
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Ivvaa:
Pokud konečným funkcionálem míníme takový, který nabývá pouze konečných hodnot, pak skutečně  je konečný funkcionál, neboť
je konečný funkcionál, neboť
1) 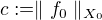 je konečné číslo (protože
je konečné číslo (protože 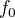 je ohraničený l. f. v
je ohraničený l. f. v  ),
),
2) pro libovolné  je
je 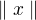 konečné číslo ,
konečné číslo ,
3) součin 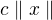 dvou konečných čísel je konečné číslo. :-)
dvou konečných čísel je konečné číslo. :-)
Nebo má snad pojem konečnosti funkcionálu jiný obsah, než jak jsem napsal ?
Offline
#5 03. 06. 2013 13:37
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Rumburak: takže se dá brát ohraničený = konečný? to pak určitě jo...
Offline
#6 03. 06. 2013 13:58
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Rumburak:
Kde berete jistotu, že platí 2) ? Například prvek 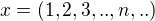 (uvažujeme-li nekonečně dimenzionální prostor) konečnou normu nemá.
(uvažujeme-li nekonečně dimenzionální prostor) konečnou normu nemá.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#7 03. 06. 2013 16:22
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Honza90:
Jistotu beru z předpokladu, že  , kde
, kde  je lineární normovaný prostor, k čemuž jsem si z dalšího kontextu domyslel,
je lineární normovaný prostor, k čemuž jsem si z dalšího kontextu domyslel,
že tato norma je značena  (taková "licence" je ve funkcioální analýze běžná) .
(taková "licence" je ve funkcioální analýze běžná) .
Že na lineárním normovaném prostoru  nabývá jemu příslušná norma
nabývá jemu příslušná norma  pouze konečných (a sice nezáporných)
pouze konečných (a sice nezáporných)
hodnot, je obsaženo v definici LNP resp. v definici normy na lin. prostoru.
Zamozřejmě, že si mohu zavést lineární prostor  a na něm funkci označenou
a na něm funkci označenou  , která bude nabývat i nekonečných hodnot,
, která bude nabývat i nekonečných hodnot,
ale pak už by nebylo možno říci, že by usp. dvojice  byla LNP. Ale mohlo by se stát, že by funkce
byla LNP. Ale mohlo by se stát, že by funkce 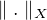 vzniklá
vzniklá
zúžením funkce  na nějaký podprostor
na nějaký podprostor  už splňovala definici normy na lin. postoru
už splňovala definici normy na lin. postoru  .
.
Pokud jsem něco napsal ne dosti srozumitelně, ptejte se. Případně rozveďte podrobněji Vámi uvedený příklad, tj. uveď te, o který
lin. prostor se v něm jedná a jak je definována Vámi zmiňovaná "norma".
Offline
#8 03. 06. 2013 17:17
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
takže se dá brát ohraničený = konečný? to pak určitě jo...
Záleží na tom, jak máte tyto pojmy definovány.
Pokud jde o "konečnost" funkcionálu: Já jsem se s její definicí, striktně vzato, nesetkal a o jejím možném obsahu jsem vyslovil
pouhou doměnku převzatou z těch partií matematiky, kde je přípustné, aby funkce nabývající číselných hodnot nabývala i hodnot
nekonečných (teorie Lebesgueova integrálu, analýza v komplezním oboru).
Ohraničenost LINEÁRNÍHO funkcionálu podle mne znamená, že má konečnou normu (supremum z |f(x)| přes jednotkovou kouli),
což je ekvivalentní s jeho spojitostí.
Pokud by moje vidění těch definic bylo správné (funkcionální analysou jsem se už dlouho nezabýval a leccos bych si potřeboval
připomenout), pak každý lineární funkcionál je konečný, ale v prostorech nekonečné dimense platí, že ne každý lineární funkcionál
je spojitý a tedy ne každý je ohraničený.
Offline
#9 03. 06. 2013 18:12
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Rumburak:
Já bych se chtěl zeptat, odkud plyne tato nerovnost. Je-li  NLP,
NLP, 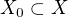 a
a 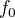 funkcionál definovaný na
funkcionál definovaný na  a
a  je prodloužením
je prodloužením 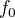 na
na  . Potom platí:
. Potom platí: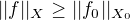 respektive
respektive 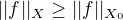
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#10 04. 06. 2013 09:38
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
↑ Honza90:
Měli bychom asi doplnit předpoklad, že  je spojitý lineární funkcionál .
je spojitý lineární funkcionál .
Nerovnost
(0) 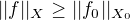
plyne z definice normy spojitého lineárního funkcionálu:
(1) 
(nebo ekvivalentně 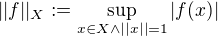 ) . Analogicky
) . Analogicky
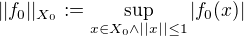 ,
,
tedy
(2) 
Množina, přes kterou se "počítá" supremum, je v případě (1) větší než v případě (2) , protože  .
.
Odtud plyne (0).
Offline
#11 04. 06. 2013 10:02 — Editoval Brano (04. 06. 2013 10:07)
Re: Hanh-Banachova věta v normovaném tvaru - důkaz
Vo funkcionalke "ohraniceny"="spojity"
odaz na wiki
"ohraniceny" zrejme preto, ze ma ohranicene hodnoty na jednotkovej guli - co sa vyuzije na definovanie operatorovej normy.
Tu "konecnost" sme tu uz niekde diskutovali a dosli sme k nazoru, ze je to asi tak, ze to znamena "nenadobuda nekonecne hodnoty" - co asi autor chce specialne zdoraznit, lebo nekonecne hodnoty pri normach sa obcas povoluju.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hanh-Banachova věta v normovaném tvaru - důkaz

