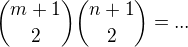Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 06. 2013 14:50
kombinatorika
Zdravím. Mám tu jeden příklad a moc nevím jak na něj.
"Obdélník je rozdělený vodorovnými a svislými úsečkami na m × n čtverců velikosti 1 × 1. Kolik různých obdélníků je tímto dělením určeno?"
Podle mě takových obdélníků může být strašně moc, různých velikostí a tvarů a nemám vůbec ponětí jak to nějak zesystematizovat...
Díky za případný rady.
Offline
#2 04. 06. 2013 15:28
Re: kombinatorika
Zase až tak složité to není - tedy pokud se na mě neprojevil den v práci útlumem.
Jistě platí S=m*n. Jakýkoliv jiný obdélník poskládaný ze vytvořených čtverců bude mít jistě stejný obsah. To znamená, že musíš jen nalézt taková n_i, m_i, pro která platí, že n_i*m_i=S.
Tedy jinak řečeno najdeš si všechny dělitete čísla S a z něj vybereš jen ty dvojice, jejichž součin je opět S. Zná se to těžké? Vůbec ne - stačí ke každému děliteli n_i přiřadit m_i=S/n_i.
Zdánlivě je to neřešitelné, ale existuje něco jako Eulerova funkce , která vrátí k číslu n počet čísel menších než n s n nesoudělných. Počet dělitelů tak získáš jako:
Nakonec si ještě rozmysli, že když pojedeš po uspořádaných dělitelích, dostaneš vždy dvě dvojice stejné. Takže výslednou hodnotu musíš podělit dvěma. Výjimkou je případ, kdy bude existovat a takové, že S=a*a - to se pak takhle započítá jen jednou (to lze ošetřit např. zaokrouhlováním).
Доктор сказал «в морг» — значит в морг!
Offline
#5 04. 06. 2013 15:42
Re: kombinatorika
↑ kexixex:
Ano, taky si myslim, ze to je uloha ve stylu "kolik obdelniku je na obrazku"...
a otazka "kolik obdelniku ma levy horni roh ve ctverci 1,1" mi zni trochu jako "Jaký je zvuk padajícího stromu v lese kde nikdo není?" ---> Vůbec mi nepomohla ;).
Offline
#6 04. 06. 2013 15:47
Re: kombinatorika
↑ Mythic:
Jak jsem vymyslel - Ze zadání;-) Je-li obdélník rozdělen na m x n čtverců o rozměrech 1x1, má zřejmě obsah m*n. Tak nějak se mi zdálo, že ti jde o přeuspořádání těch čtverců na jiný obdélník (to je totiž mnohem zajímavější). Eulerovu funkci najdeš na Wikipedii.
_______________________
Jinak je možné, že se ptáš na úlohu mnohem jednodušší, totiž na to, kolik různých obdélníků můžeš to vzniklé čtvercové sítě nakreslit. Systematizování je jednoduché - představ si, že si stranu n necháš konstantní a m o jeden zkrátíš. Vzniklý obdélník můžeš jednou posunout, máš tedy dvě možnosti. Když zkrátíš stranu o dva dílky, máš tři možnosti,... až pro délku jeden dílek máš m možností.
Tedy celkem pro umístění "podobdélníku" s proměnnou stranou m máš 1+2+...+m = m*(1+m)/2 možností.
Zcela analogickou úvahu můžeš udělat pro stranu n. No a protože jde o změny "volně kombinovatelné", počet všech možných kombinací "každý s každým" získáš vynásobením:
(čili nuda, ne? ;-) )
Доктор сказал «в морг» — значит в морг!
Offline
#7 04. 06. 2013 16:00 — Editoval Mythic (04. 06. 2013 16:02)
Re: kombinatorika
To zní docela dobře, připadá mi ale, že v tom jsou zahrnuty jen odbélníky, které mají libovolnou výšku, ale pevně danou šířku - totiž m, respektive n. Kde se v tom skrývají třeba obdélníky 1*2 ?
Jinak tedy ještě abych byl kompletní. Našel jsem u nás výsledek (m+1 nad 2) * (n+1 nad 2), který mi připadá dost prapodivný.
Offline
#8 04. 06. 2013 16:11
Re: kombinatorika
↑ Mythic:
uvedeny vysledek je stejny jako uvadi Formol, protoze  , pro m stejne..
, pro m stejne..
K mymu "postupu": obdelniku, ktery maj levej horni roh ve ctverci 1,1 je m*n, postupne to spoctes pro ctverce i,j, kde i=1..m; j=1..n, takze vysledek je  stejnej...
stejnej...
Offline
#9 04. 06. 2013 16:14
Re: kombinatorika
Ok, nejsrozumitelnejsi (nejpredstavitelnejsi) mi pripada postup od Formol. Pořád ale nechápu to co sem psal výš:
"Připadá mi ale, že v tom jsou zahrnuty jen odbélníky, které mají libovolnou výšku, ale pevně danou šířku - totiž m, respektive n. Kde se v tom skrývají třeba obdélníky 1*2 ?"
Offline
#10 04. 06. 2013 16:54
Re: kombinatorika
↑ Mythic:
Ta úvaha je naprosto stejná, jako když - možná si to tak lépe představíš - házíš dvěma kostkami. Na jedné máš šest možností, na druhé máš šest možností a počet dvojic dostaneš vynásobením (vlastně počet prvků "tabulky" všech kombinací). Tady je to stejné - obdélník ti určí dvě strany v zásadě nezávisle (zkus si to chvíli kreslit). Takže si můžeš nezávisle na sobě určit, přes které "sloupce" půjde jedna strana a přes které "řádky" druhá.
Доктор сказал «в морг» — значит в морг!
Offline
#11 05. 06. 2013 09:43 — Editoval Rumburak (05. 06. 2013 09:54)
Re: kombinatorika
Zdravím v tématu.
Ze zadání "Obdélník je rozdělený vodorovnými a svislými úsečkami na m × n čtverců velikosti 1 × 1" plyne,
že celkem máme dejme tomu m+1 přímek vodorovných (jejich množinu označme V) a n+1 přímek svislých
(jejich množinu označme V), na nichž leží strany jednotlivých obdélníků včetně obdélníka výchozího i včetně
oněch m*n čterců.
Každý z těchto obdélníků je jedoznačně určen zvolenou dvojicí navzájem různých přímek z V a (k ní) zvolenou
dvojicí navzájem různých přímek z S.
Dvojice navzájem různých přímek z V jsou kombinacemi 2. tř. z m+1 prvků ... atd.
Výsledek:
Offline