Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 06. 2013 15:09 — Editoval Blackflower (12. 06. 2013 15:17)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: kvadratické rovnice
↑ simushka8: Ahoj,
vypočítala si korene?
Označme si korene  ,
, 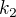 . Keď medzi ne vložíme dve čísla, bude to vyzerať takto:
. Keď medzi ne vložíme dve čísla, bude to vyzerať takto: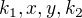
Štyri čísla majú byť po sebe idúce členy GP, teda musí platiť, že každý člen bude q-násobkom predchádzajúceho: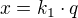
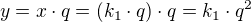
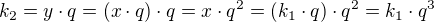
Offline
#3 12. 06. 2013 15:13
Re: kvadratické rovnice
↑ simushka8:
kořeny kvadratické rovnice jsou první resp. čtvrtý člen geometrické posloupnosti. Z těchto členů získáš kvocient posloupnosti a druhý a třetí člen
Offline
#4 12. 06. 2013 15:20 Příspěvek uživatele darkzprior byl skryt uživatelem darkzprior. Důvod: zle
#6 12. 06. 2013 15:25
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: kvadratické rovnice
↑ simushka8: Ako píše ↑ Pivňa:, korene by mali vyjsť 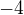 a
a 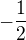 .
.
Povedzme, že  ,
, 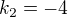 . Vložíme medzi tieto korene ďalšie dve čísla:
. Vložíme medzi tieto korene ďalšie dve čísla: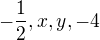
Keď vynásobíme prvý koreň (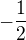 ), nejakým číslom
), nejakým číslom  , dostaneme
, dostaneme  .
.
Keď vynásobíme  tým istým
tým istým  , dostaneme
, dostaneme  .
.
Keď vynásobíme  tým istým
tým istým  , dostaneme
, dostaneme 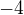 .
.
Offline
#8 12. 06. 2013 15:37
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Offline
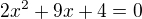 vložte dvě čísla tak, aby spolu s těmito kořeny vznikly první čtyři členy geometrické posloupnosti
vložte dvě čísla tak, aby spolu s těmito kořeny vznikly první čtyři členy geometrické posloupnosti


