Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 06. 2013 17:15 — Editoval Aktivní (13. 06. 2013 17:16)
Lambertova W funkce
Ahoj, nikde jsem se nedohledal postupu jak číselně zjistit W(x) (Lambertova W funkce).
Z Wikipedie moc moudrý nejsem, našel jsem tam například Taylorovu řadu:
Které ale ani nerozumím, protože nevím co symbolizuje na nula 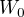 .
.
Jak tedy zjistit funkční hodnotu té funkce např. v bodě 6 ?
Offline
- (téma jako vyřešené označil(a) Aktivní)
#2 13. 06. 2013 17:31
Re: Lambertova W funkce
↑ Aktivní:
Ahoj
Podle toho, jak jsem pochopil definici této funkce, tak bych řekl zhruba toto.
Taylorův rozvoj je v bodě šest k ničemu, nebot řada konverguje jen na intervalu -1/e,1/e.
Ta funkce je navíc definovaná i pro komplexní čísla, tedy v libovolném bodě teoreticky nabývá více hodnot (je mnohoznačná)- ta nula tedy značí jenom tu část funkce, která lze považovat za funkci v normálním smyslu.
Jelikož je funkce definovaná jako 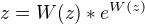
tak hodnotu v libovolném bodě můžeme získat libovolnou numerickou metodou (přesné číslo analyticky nenajdem)
Tedy necht y je hodnota funkce v bodě 6. pak je třeba řešit rovnici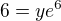
Offline
#3 15. 06. 2013 15:03 — Editoval Aktivní (15. 06. 2013 15:06)
Re: Lambertova W funkce
Aha.
Stejně mi pak není jasné k čemu řešení ve tvaru 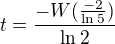 může být užitečné, když má od číselného vyjádření tak hodně daleko.
může být užitečné, když má od číselného vyjádření tak hodně daleko.
Jestli to dobře chápu, při hledání kořenů například rovnice  je nejefektivnější metoda např. metoda tečen a né metoda skrze Lambertovu W funkci. Je to tak?
je nejefektivnější metoda např. metoda tečen a né metoda skrze Lambertovu W funkci. Je to tak?
Offline
#4 15. 06. 2013 17:30
Re: Lambertova W funkce
Tak pokud jde o hledání číselného výsledku tak ano.
Takovéto výsledky se podle mě uplatňují ve výpočetní technice (některé programy třeba umějí tuto funkce vyčíslit) a nebo třeba při nějakých úpravách výrazů. Každopádně při hledání číselného výsledku (když prostě počítáš jen s kalkulačkou a papírem) tak je podle mě metoda tečen lepší.
Další využití jak koukám je, že tato funkce je řešením některých diferenciálních rovnic - dostávám hezčí zápis, než kdybych tuto funkci nepoužil.
Offline
#6 28. 12. 2023 19:15
Re: Lambertova W funkce
↑ Sherlock:
2^t = 5t
1/5 = t*2^(-t)
e^ln(2)=2
-1/5*ln(2) = -t*ln(2) * e^(-t*ln(2))
W(-1/5*ln(2)) = W(-t*ln(2) * e^(-t*ln(2)))
W(-1/5*ln(2)) = -t*ln(2)
t = -W(-1/5*ln(2))/ln(2)
t = -productlog(-1/5*log(2))/log(2) = 0.2354557100710055297910789920279545099338639544667685177035489804
===
Zkouška: Wolframalpha.com
2^t = 2^0.2354557100710055297910789920279545099338639544667685177035489804 = 1.1772785503550276489553949601397725496693197723338425885177449022
5t = 5*0.2354557100710055297910789920279545099338639544667685177035489804 = 1.177278550355027648955394960139772549669319772333842588517744902; OK
Nepočítám tak snadno jako když dýchám a někdy i chybuji.
Offline