Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 06. 2013 12:35
grupa S8
Dobrý den. Lámu si hlavu s následujícím: Určete počet prvků řádu 4 v grupě permutací S8.
Začal jsem zkoumáním prvků řádu 4 v S4. Zjistil jsem, že v S4 jsou řádu 4 ty prvky, kde žádná pozici není sama na sobě a permutace má lichou signaturu. Počet prvků, kde pozice není sama na sobě je 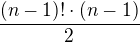 . Kolik z nich má obecně lichou signaturu nevím a asi to není důležité. V S8 musí být vše přeházené s lichou sgn na 4 až 8 pozicích. Dál, už nevím, co s tím, ani si nejsem jistý, jestli to co tvrdím, je správné.
. Kolik z nich má obecně lichou signaturu nevím a asi to není důležité. V S8 musí být vše přeházené s lichou sgn na 4 až 8 pozicích. Dál, už nevím, co s tím, ani si nejsem jistý, jestli to co tvrdím, je správné.
Druhý postup, který by mohl někam vést. Každý prvek řádu 3, se dá vyrobit přehozením nějaké pozice 3x tam, kde předtím nebyla. Např.
1234
první přehození: 1 s 2
2134
druhé přehození: 1 s 3
2314
třetí přehození: 1 s 4
2341
což je prvek řádu 4
Výběr první dvojice je z 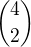 výběr druhé z
výběr druhé z 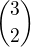 atd. Prvek 2341 se dá vyrobit i jinak, ale vždy to lze i takto. Po troše počítání mi příjde, že 2341 lze sestrojit třema různými cestami, které dodržují tento postup.
atd. Prvek 2341 se dá vyrobit i jinak, ale vždy to lze i takto. Po troše počítání mi příjde, že 2341 lze sestrojit třema různými cestami, které dodržují tento postup.
Pokud by to byla pravda, v S8 by stačilo tuhle množinu rozšířit o možnosti na dalších pozicích, kde se buď nic neděje, nebo tam dochází k jednomu nebo třem přehozením.
Takže ani k dílčímu výsledku jsem se vlastně nedobral, ačkoliv jsem nad tím strávil až příliš mnoho času. Pokud máte chuť , poraďte mi, jak postupovat. Hodně by mě zajímal výsledek, resp. postup k němu.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#2 23. 06. 2013 17:18 — Editoval vanok (23. 06. 2013 17:20)
Re: grupa S8
Ahoj ↑ Honza90:,
V tejto grupe mas uz vsetki cykly dlzky 4. Tak urci kolko ich je.
Inac vieme, ze ak nejaky prvok symetrickej grupy je vytvoreny cyklamy (zo disjuktnymy orbitmy) tak jeho rad je NSN vsetkych vytvarajucych cyklov.
Ake su moznosti na to v  ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 23. 06. 2013 18:10 — Editoval vanok (23. 06. 2013 18:14)
Re: grupa S8
Mozes skusit, ako bonus, najst odpoved na tuto otazku: Aky je najvadci mozny rad nejakeho prvku v tejto grupe?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 23. 06. 2013 20:44
Re: grupa S8
↑ vanok:
Podle toho co pises bude nejvetsi rad asi 15=nsn(5,3)..cyklus delky 5 a cyklus delky 3, je tak?
Jinak te prvni rade moc nerozumim. O jake grupe mluvis, ze v ni jsou vsechny cykly delky 4? Nebo znamena delka cyklu neco jineho nez z kolika se sklada prvku?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#5 23. 06. 2013 21:01 — Editoval vanok (23. 06. 2013 21:03)
Re: grupa S8
no co sa tyka 15 mas pravdu...napr (512345)(678) vyhovuje.
Stale pisem o grupe 
Ty mas vycislit prvky radu 4.
Popisal som ti jednu ich klasu.
Kolko je takych prvkov?
A take ine klasy najdes, vdaka vlasnosti o NSN.( su tri)
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 23. 06. 2013 21:28 — Editoval vanok (24. 06. 2013 11:15)
Re: grupa S8
Tak este mala pomoc
Cyklus ma 4 pohyblive prvky a 4 fixne.
Ich pocet urcis tak ze z 8 prvkov vyberes lubovolne 4, je ich 
a akoze kazdy cyklus sa moze pisat 4my sposobmy napr.  su 4 mozne zapisy pre ten isty cyklus.
su 4 mozne zapisy pre ten isty cyklus.
To ti da 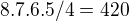 moznych takych cyklov.
moznych takych cyklov.
Iny priklad inej kategorii
Skus to sam dokoncit.
Ozaj co studujes? (skola, rocnik, predmet )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 23. 06. 2013 21:35 — Editoval Honza90 (23. 06. 2013 21:48)
Re: grupa S8
↑ vanok:
422, 4211, 41111 budou ty prvky radu 4, sem jsem se dostal aji svym primitivnym postupem, ale uz jsem to spravne nevycislil. Studuji mat inzenyrstvi, VUT brno, 2-3 rok bc.
Ty pracujes jako odborny matematik? To je me vysnene povolani.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#9 23. 06. 2013 22:03
Re: grupa S8
tie prvky co pises nevyzeraju ako treba.
tam ti aj priklady na tie dve triedy co musis vysetrit
(1234)(56)(78)
(1234)(5678)
vidis ze ta jednoducha vlasnost s NSN funguje...
Ano pracujem ako matematik... no ale je lepsie robit aplikovanu matematiku, co sa tyka platu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 24. 06. 2013 02:07 — Editoval Honza90 (24. 06. 2013 02:57)
Re: grupa S8
↑ vanok:
tedy pripustne prvky vyjadrene v cyklech jsou:
(1234) ma 8*7*6*5/4=420 zpusobu
a) (1234)(5)(6)(7)(8) ... 420*1
b) (1234)(56)(7)(8) ... 420*4*3/4=1260
c) (1234)(56)(78) ... 420*4*3/4=1260
d) (1234)(5678) ... 420*4*3*2/4=2520
celkem 5460 prvku radu 4.
diky za radu ;)
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#12 24. 06. 2013 03:00 — Editoval vanok (24. 06. 2013 03:04)
Re: grupa S8
Pripad a) c) je dobre vycislineny.
Druhe dva treba opravit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 24. 06. 2013 08:40 — Editoval vanok (24. 06. 2013 09:25)
Re: grupa S8
D) treba vydelit 2!=2, lebo inac kazdy cyklus je napisany dva krat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 24. 06. 2013 11:10
Re: grupa S8
nie, argument je: dva disjonktne cykly komutuju.
A tak kazdy prvkok sa da napisat dvomi sposobmy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 24. 06. 2013 11:14 — Editoval vanok (24. 06. 2013 11:24)
Re: grupa S8
↑ Honza90: tu si dal jednu otazku, na ktoru som ti dal vyssie priklad
↑ vanok:
kazdy cyklus sa moze pisat 4my sposobmy napr.  su v S8, 4 mozne zapisy pre ten isty cyklus.
su v S8, 4 mozne zapisy pre ten isty cyklus.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 24. 06. 2013 12:27 — Editoval vanok (24. 06. 2013 12:31)
Re: grupa S8
Prvok ako (1234)(56) je vytvoreny z dvoch disjonknych cyklov ( tie komutuju)
Trieda takych prvkov ma ((8.7.6.5/4)(4.3)/2).2/2 =8!/(4.2.2!) ktorych je ako si aj sam urcil 2520.
Posledna2 je vdaka komutativite cyklov
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 24. 06. 2013 12:58 — Editoval vanok (24. 06. 2013 12:59)
Re: grupa S8
Ako vidim tazke veci rozumies velmi dobre. À tie lahke nie.
Vsak ide o cisto kombinacny problem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 24. 06. 2013 13:25
Re: grupa S8
vsak to sedi z tym co som vyssie pisal.
Kdemas problem?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 24. 06. 2013 13:40
Re: grupa S8
a dostanes 8!/(2^3.3!.2!)=420
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
