Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 07. 2013 12:49
Diferenciální rovnice
Ahoj, mam zadani: Reste cauchyho ulohu, a chci se zeptat co delam spatne, protoze me vychazi pod odmocninou zaporne cisla.
Dekuji.![kopírovat do textarea $y'=\frac{xy^2-x}{x^2y-y} [y(1/2)=-2]$](/mathtex/53/53cceb23f4daa0ebc59694ec5ba222bf.gif)
 po spocitani integralu
po spocitani integralu![kopírovat do textarea $\sqrt[2]{y^2-1}=\sqrt[2]{x^2-1}*C$](/mathtex/2d/2d15410e2f8537249896e9482fea3099.gif)
![kopírovat do textarea $\frac{\sqrt[2]{y^2-1}}{\sqrt[2]{x^2-1}}=C$](/mathtex/36/366cb7cf5e8d8e6f3480bd2e6f7e2c99.gif) kdyz dosadim za x=1/2 a y=-2 vyjde pod odmocninou zaporne cislo.
kdyz dosadim za x=1/2 a y=-2 vyjde pod odmocninou zaporne cislo.
Offline
- (téma jako vyřešené označil(a) frantax)
#2 12. 07. 2013 13:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Diferenciální rovnice
Zdravím,
ve vzorcích integrování by se měla objevit absolutní hodnota (to se běžně zapomíná) - jinak jsem celý postup nekontrolovala, ale pro úpravu bych nejdřív řádek "po spočítání integrálu" vynásobila 2 a také je dobré přeznačovat C (jednou je C, potom je C1=ln(C)).
Bude to tak v pořádku? Děkuji.
Offline
#4 12. 07. 2013 16:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Diferenciální rovnice
↑ frantax:
absolutní hodnotu třeba mít (zeptám se potom v sekci podpory (nejen) MAW), proč není absolutní hodnota.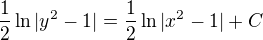 pokud mám jen počítat C, tak mohu rovnou dosazovat hodnoty z počáteční podmínky.
pokud mám jen počítat C, tak mohu rovnou dosazovat hodnoty z počáteční podmínky.
Pokud bych měla vyjádřit 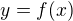 , tak bych ještě upravovala:
, tak bych ještě upravovala:

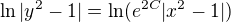 , zde přeznačím
, zde přeznačím 
 a v tomto kroku si nemyslím, že mohu absolutní hodnotu jen tak odmyslit, ale postupně - tak bych to viděla.
a v tomto kroku si nemyslím, že mohu absolutní hodnotu jen tak odmyslit, ale postupně - tak bych to viděla.
Offline
#6 12. 07. 2013 17:23
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Diferenciální rovnice
Ahoj
označme 

Když bude platit 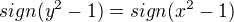 , odstraníme absolutní hodnotu tak, že
, odstraníme absolutní hodnotu tak, že 
Když bude platit  ,odstraníme absolutní hodnotu tak, že
,odstraníme absolutní hodnotu tak, že 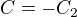
Takže stačí z  udělat
udělat  (a pořešit, zda C=0 je taky řešením).
(a pořešit, zda C=0 je taky řešením).
MAW jsem nezkoumal, on neukazuje, z jakého oboru konstantu bere?
Offline
#7 14. 07. 2013 09:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Diferenciální rovnice
↑ Hanis:
Také pozdrav :-) Děkuji, určitě to tak může být.
V tomto tématu jsem nakonec úpravy pro bezrizikovost absolutní hodnoty snad našla.
MAW jsem nezkoumal, on neukazuje, z jakého oboru konstantu bere?
statistiky využití MAW z Opavy kazím nezodpovědným přístupem k využití - na hlavní stránce ihned přecházím přes levý dolní roh a zkoumám "Geolocation". Ukazuje skvěle :-).
Tuto úlohu jsem prošla přes kroky integrování apod. (zde nebyl problém s absolutní hodnotou), přímo v řešení dif. rovnice podrobnosti o konstantě neuvádí.
Ono je to stejně tak - určitě bych MAW doporučila, pokud nevím, jak začít (typ dif. rovnice, úprava na použitelný tvar, základní kroky), integrování (také základní kroky), případně náhled na výsledek. Ale jak píše i sám vážený autor ohledně různých úskalí, tak podrobné řešení bych prováděla ručně - jelikož zde např. MAW neprovádí počáteční rozbor zadání, def. obory, nulové body dif. rovnice ohledem na f(x), g(y) atd. Zde je takových momentů celkem dost.
Zápis, který nabízí jako řešení, se mi jeví úpravou na "nejpohodlnější tvar na derivování", je bez komentáře ohledně def. oborů (ovšem to jde napravit průchodem přes další sekce MAW).
Potíž je i v tom, že WA nepoužívá absolutní hodnotu ani v takovém případě (integrování 1/x). Lepší závěr, než závěr hodnocení kolegy jarrro ještě nikdo nevymyslel :-)
Navíc tato úloha požadovala nalezení C pro počáteční podmínku, což by raději provedla hned 1. řešením s absolutní hodnotou (která v místních poměrech má být), bez dalších úprav (vždy je v úpravách riziko chyby).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)