Matematické Fórum

simcilka · 05. 09. 2013 14:40

Ahoj, pomaham kamaradce a ja jsem ve škole nikdy nebrala součet řady, tak ani nevim jak ji mam vysvětlit tuhle řadu.
$\sum_{n=3}^{\infty}\ln(1-\frac{4}{n^{2}})$

nasla jsem si vzorec 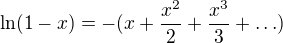$\ln(1-x)=-(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+\ldots)$ dosadila jsem ale dale vuebc nevim co s tim, nevim jestli to muzu takhle zasubstitovat, nebo jak:(

dosadila jsem si do prvnich par clenui a vyslo mi že součet řady pujde k zapornýmu čislu, které bude větší než -1. Můžete mi to prosim nekdo vyvetlit jak mam postupovat?

jarrro · 05. 09. 2013 15:39 — Editoval jarrro (05. 09. 2013 15:40)

platí
$\ln{$1-\frac{4}{n^2}$}=\ln{$\frac{n^2-4}{n^2}$}=\ln{$n-2$}-2\ln{$n$}+\ln{$n+2$}$
súčet nekonečného radu je limita postupnosti jeho čiastočných súčtov podďme ten čiastočný súčet zistiť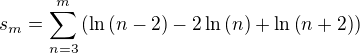
$s_m=\sum_{n=3}^{m}{$\ln{\(n-2$}-2\ln{$n$}+\ln{$n+2$}\)}$
označme $k:=\sum_{n=5}^{m-2}{$\ln{\(n$}\)}$
pretože uvažujeme konečné súčty, je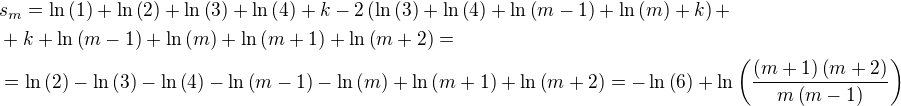
$s_m=\ln{$1$}+\ln{$2$}+\ln{$3$}+\ln{$4$}+k-2$\ln{\(3$}+\ln{$4$}+\ln{$m-1$}+\ln{$m$}+k\)+\nl +k+\ln{$m-1$}+\ln{$m$}+\ln{$m+1$}+\ln{$m+2$}=\nl =\ln{$2$}-\ln{$3$}-\ln{$4$}-\ln{$m-1$}-\ln{$m$}+\ln{$m+1$}+\ln{$m+2$}=-\ln{$6$}+\ln{$\frac{\(m+1$$m+2$}{m$m-1$}\)}$
argument posledného logaritmu ide k jednej teda celý logaritmus ide k nule nekonečný súčet je teda $-\ln{$6$}$

Rumburak

↑ simcilka:

Ahoj. Zkusme ten součet řady určit "z definice". Označme

$S_m = \sum_{n=3}^{m}\ln$1-\frac{4}{n^{2}}$$ ,

tedy pro dostatečně velká $m$ bude

$S_m :=\ln \prod_{n=3}^{m}$1-\frac{4}{n^{2}}$ = \ln \prod_{n=3}^{m}\frac{(n+2)(n-2)}{n^{2}} =\ln $\prod_{n=3}^{m}\frac{n+2}{n}\prod_{n=3}^{m}\frac{n-2}{n}$ =\\=\ln$\frac{5}{3}\,\frac{6}{4} ... \frac{m+2}{m}\cdot \frac{1}{3}\,\frac{2}{4} ... \frac{m-2}{m}$ = \ln $\frac {(m+1)(m+2)}{3\cdot 4}\cdot \frac {1\cdot 2}{(m-1)m}$$ ,

odtud už není těžké zjistit, že $\lim_{m \to \infty}S_m = - \ln 6$ .

Matematické Fórum

#1 05. 09. 2013 14:40

součet řady

#2 05. 09. 2013 15:39 — Editoval jarrro (05. 09. 2013 15:40)

Re: součet řady

#3 05. 09. 2013 15:40 — Editoval Rumburak (05. 09. 2013 15:55)

Re: součet řady

Zápatí