Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 09. 2013 19:47
Konstanty Antoinovy rovnice.
Teď jsem řešil tento problém a ač není obtížný připadala mi tato úloha zajímavá a tak ji zveřejňuji.
Antoine rovnice popisuje vztah mezi tlakem páry a teplotou čisté látky.
U nás používáme tuto variantu [1] s přirozeným logaritmem: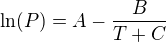
Teplotu zadáváme ve °C a výsledek máme v kPa (absolutních).
Potřeboval jsem zjistit pro určitou látku konstanty 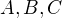 .
.
Našel jsem je, ale zdroj používá jinou variantu [2] s logaritmem o základu 10: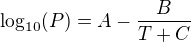
A aby to nebylo jednoduché, tak vypočítaný tlak je v barech (absolutních) a teplotu zadávají v Kelvinech.
A teď úkol.
Vypočítejte nové konstanty 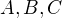 ze zjištěných pro naši variantu [1] rovnice.
ze zjištěných pro naši variantu [1] rovnice.
Offline
#2 23. 09. 2013 18:57 — Editoval mák (23. 09. 2013 19:34)
Re: Konstanty Antoinovy rovnice.
Asi ta úloha není příliš zajímavá, a nebo není tak lehká jak jsem si myslel.
Zopakuji zadání, ale tentokrát jej podrobněji rozepíšu.
Úkolem je vypočítat koeficienty ![kopírovat do textarea $[A_{1},B_{1},C_{1}]$](/mathtex/a8/a8217d7d283b697222c3e83e11b3afa8.gif) pro rovnici [1] kde teplota je zadaná ve °C a tlak vychází v kPa:
pro rovnici [1] kde teplota je zadaná ve °C a tlak vychází v kPa: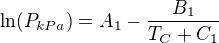
Známe však koeficienty ![kopírovat do textarea $[A_{2},B_{2},C_{2}]$](/mathtex/50/503d265709e9648a19596ddddb3788d1.gif) pro tu samou látku, ale pro tuto rovnici [2] kde teplota je zadaná v Kelvinech a tlak vychází v barech:
pro tu samou látku, ale pro tuto rovnici [2] kde teplota je zadaná v Kelvinech a tlak vychází v barech: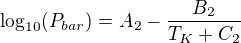
První krok - využijeme poznatku, že teplota ve stupních Celsia má stejný přírůstek jako v Kelvinech, ale obě stupnice jsou posunuté o konstantu 273.15. Takže konstanta C2, která sousedí s teplotou, bude pravděpodobně posunutá o stejnou hodnotu.
Převedeme si teplotu na jednu stranu (přesuneme tam i konstantu C), nejprve rovnice [1]: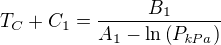
A nyní i rovnici [2]: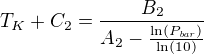
Obě rovnice musí dávat stejné výsledky - první ve stupních Celsia a druhá v Kelvinech (to byl požadavek).
Takže levé strany musí být identické: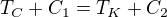
Protože:
Pak: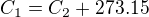
A jedna konstanta je vyřešená.
Teď už to půjde snadno.
Offline
#3 23. 09. 2013 19:26 — Editoval mák (23. 09. 2013 19:36)
Re: Konstanty Antoinovy rovnice.
Zbyly nám pravé strany - ty se taky musí rovnat: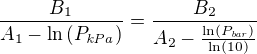
Ale máme tam jiné jednotky. Víme že: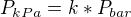
Přičemž v tomto případě je: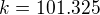
Dosadíme: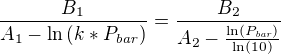
Což je stejné jako: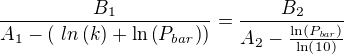
Máme tedy jednu rovnici.
Neznámé máme však dvě, musíme ještě jednu vyrobit. Využijeme poznatku, že pokud libovolně změníme hodnotu tlaku, pak se obě strany musí stále rovnat. Posuneme tlak o hodnotu z: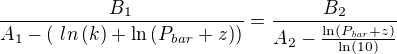
Druhá rovnice je na světě a soustava je řešitelná s výsledkem: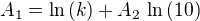
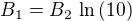
Poznámka: při opisování jsem udělal několik chyb (proměnné mám jinak značené), snad jsem je všechny opravil.
Offline