Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 10. 2013 18:57
Rýchlosť
Dobrý deň. Mohol by mi prosím niekto vysvetliť ten pojem ? Akosi mi niečo uniká.
Ak mám povedzme pohyb charakterizovaný parametricky rovnicami 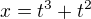 ,
, 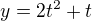 , tak ako mám určiť vektor rýchlosti v ľubovoľnom bode ? Je veľkosť rýchlosti rovná veľkosti vektora rýchlosti ?
, tak ako mám určiť vektor rýchlosti v ľubovoľnom bode ? Je veľkosť rýchlosti rovná veľkosti vektora rýchlosti ?
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 04. 10. 2013 20:23 — Editoval KennyMcCormick (04. 10. 2013 22:38)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Rýchlosť
Je veľkosť rýchlosti rovná veľkosti vektora rýchlosti ?
Správně.
ako mám určiť vektor rýchlosti v ľubovoľnom bode ?
Všimni si, že 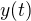 je prostá funkce - čas je jednoznačně určený y-ovou polohou:
je prostá funkce - čas je jednoznačně určený y-ovou polohou:
Protože rychlost je jednoznačně určená časem, a čas je jednoznačně určený y-ovou polohou, stačí ti k určení rychlosti y-ová poloha (x-ovou souřadnici nepotřebuješ).
Teď polohový vektor zderivuješ:

A dosadíš za  :
: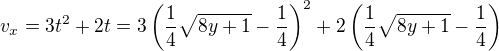
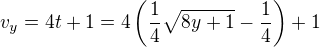
Je to jasný?
EDIT: Překlep.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#3 04. 10. 2013 22:31
Offline
#4 04. 10. 2013 22:36
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Rýchlosť
...jasně, omlouvám se. Díky.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline

