Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 10. 2013 18:58
Tečna paraboly
Dobrý den,
Mohl bych Vás poprosit o radu ohledně tohoto příkladu?
Rce paraboly: 
Úkol: Nalezni tečnu paraboly, která je rovnoběžná s přímkou y=x.
Postupoval jsem:
vrcholová rce: 
vrchol:![kopírovat do textarea $[3,2]$](/mathtex/8c/8ca70752096c0d36e548c17c61e59c98.gif)
parametr: 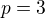
ohnisko: ![kopírovat do textarea $F[\frac{9}{2},2]$](/mathtex/3b/3ba24b9cbd69354fef17dfde0e61ebe2.gif)
řídící přímka: 
- poté jsem si vypočítal rovnici, která prochází bodem F a je kolmá k y=x, ale nejsem si
jistý, jestli dobře....
- od tohoto kroku je to nejspíš špatně
- poté jsem počítal průsečík y=13/2 - x s řídící přímkou
- vyšel mi bod M, v polovině vzdálenosti bodu M a ohniska F by měl ležet bod T(místo, kde se dotýká
tečna a parabola)
- po dosazení mi ta rovnice tečny vyšla špatně
Správný výsledek: 
Tento postup se mi zdá komplikovaný, ale je to jediný, na který jsem narazil.
Díky za rady
Offline
- (téma jako vyřešené označil(a) Martin95k)
#2 05. 10. 2013 19:16
Re: Tečna paraboly
Ahoj.
Proč tak složitě? Navíc o té parabole nepotřebuju vědět skoro nic, abych tu tečnu našel, protože už jenom informace, že je rovnoběžná s přímkou y=x mi říká, že ta rovnice tečny vypadá takto:  , kde q je zatím neznámé. Teď stačí dosadit za y do úplně první rovnice té paraboly a určit q tak, aby ta vzniklá kvadratická rovnice v x měla právě jeden kořen (protože to má být tečna), tj. diskriminant bude 0.
, kde q je zatím neznámé. Teď stačí dosadit za y do úplně první rovnice té paraboly a určit q tak, aby ta vzniklá kvadratická rovnice v x měla právě jeden kořen (protože to má být tečna), tj. diskriminant bude 0.
Offline
#3 05. 10. 2013 19:18
Re: Tečna paraboly
↑ Martin95k:
pokud je přímka rovnoběžná s danou přímkou, má rovnici 
dosadíš do rovnice paraboly a určíš  tak, aby byl diskriminat rovnice roven nule.
tak, aby byl diskriminat rovnice roven nule.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 05. 10. 2013 19:22 — Editoval gadgetka (05. 10. 2013 19:28)
Re: Tečna paraboly
rovnice tečny, která je rovnoběžná s přímkou y=x, bude mít stejnou směrnici, k=1, čili její rovnice bude 



Přímka je tečnou, jestliže D=0![kopírovat do textarea $[2(q-5)]^2-4(q^2-4q+22)=0$](/mathtex/2c/2cea7607a63bef21f0dac1375cb571aa.gif)



Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline

