Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 10. 2013 20:35
Přímá a nepřímá úměrnost
Dobrý večer,
Potřeboval bych si ujasnit výpočty v trojčlence, ale k sestavení rovnice potřebuju poznat kdy se jedná o přímou a kdy a nepřímou úměrnost, poslední cvičení jsou příklady, https://scontent-b-ams.xx.fbcdn.net/hph … =5260A29E,
úloha 4) mi vyšla zapisuji takto: 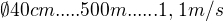
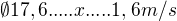
z toho jsem sestavil rovnici x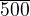 =17,6
=17,6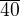 . 1.6
. 1.6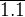
Už jsem jednoduše dopočítal, neznámou jsem si dal na levou stranu, a tvořil zlomky od spoda nahoru, ale učitelka vysvětlovala, že se musim koukat na to jaká je to úměrnost, podle toho poznam jestli mam tvořit zlomek od shora dolu nebo od zdola nahoru...
Předem díky za pomoc :)
Do latexu mi nešli dát metry krychlové a nevím jak se tam tvoří zlomky, tak snad pochopíte :)
Offline
#2 16. 10. 2013 21:00
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
Ahoj ↑ Mazarini:
Mohl by si prosím vložit nový odkaz? (nefunguje)
Pak ti vysvětlím, jak to poznáš a jak máš počítat :)
Offline
#3 16. 10. 2013 21:03
#4 16. 10. 2013 21:24 — Editoval xstudentíkx (16. 10. 2013 21:25)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Známe průměr....40 cm
známe rychlost.....1,1 m/s
a víme, že proteče 500  za hodinu
za hodinu
pak známe:
průměr...17,6 cm
rychlost....1,6 m/s
a nevíme kolik  proteče za hodinu.
proteče za hodinu.
Nejlepší bude si "zkombinovat" průměr a rychlost dohromady, proto vynásobíme rychlost*průměr (u obou dvou).
Pak sestavíme trojčlenku:
44 (40*1,1)..........500
28,16 (17,6*1,6)........x
Tak a teď musíš trochu přemýšlet, čím větší rychlost a průměr, tak tím větší bude i množství vody, která proteče a následně to platí i naopak, čím menší rychlost a průměr, tím méně vody proteče.
V případě, že platí přímá úměrnost (jako zde), budeš násobit šikmo, tedy:
28,16*500=44*x
tím dostaneš:
14080=44x
x=14080/44
x=320 
Pochopil si? :)
Offline
#5 16. 10. 2013 21:41
Re: Přímá a nepřímá úměrnost
Právě tyto postupy mi vůbec nevyhovují :/ Učitelka mi to vysvětlovala pomocí té rovnice jak jsem dělal =
= 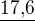 .
.  / x 11000
/ x 11000
500 40 1,1
A výsledek mi vyšel taky 320m krychlových.
Ale problem nastává u příkldu č. 3 , také to vyjde učitelka mi to ukazovala, ale já to nepochopil jednou šli šipky nahoru jednou dolů, a říkala že se musím dívat jaká to je úměrnost, jinak mi to nevyjde...
Offline
#6 16. 10. 2013 21:54 — Editoval xstudentíkx (16. 10. 2013 22:01)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Dobře, tak ti vysvětlím, jak zjistit, kdy se jedná o přímou a kdy o nepřímou :)
Přímá:
Např:
Čím větší otvor, tím víc vody proteče. Jednoduše je v tom "rovnost", čím větší= tím více.
Nepřímá:
Např.
Čím vyšší rychlostí jedu, tím kratší dobu mi trvá někam dojet. Jednoduše je v tom "nerovnost", čím vyšší=tím kratší.
Ten příklad číslo 3 se dá brát 2 způsoby, jelikož v něm můžou platit obě úměry. Pokud by si to řešil tak, že by si vynásobil čas s rychlostí, budeš řešit přímou, ale pokud by si řešil, tak jak řešíš budeš tam mít v polovině nepřímou, jelikož čím větší rychlost, tím kratší doba pokosení. Je to na tobě, vyber si způsob jaký chceš :)
Případně napiš jak si příklad číslo 3 řešil
Offline
#8 16. 10. 2013 22:19
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Ten tvůj postup mi přijde o dost složitější a nějak nemůžu přijít na to, jak ti to na něm vysvětlit. Doporučila bych ti toto:
4,5 ha.......40,5 (6,75*6)
10 ha........7x (x*7))
teď stačí 10*40,5= 405
a 4,5*7x= 31,5x
a jelikož chceme zjistit jedno x, tak 405/31,5x=12,9.
Zkus se na to kouknou.
Offline
#10 16. 10. 2013 22:43
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Ano, super job :)
Můžu se zeptat jakým si počítal způsobem?
Offline
#12 16. 10. 2013 22:58 — Editoval LukasM (16. 10. 2013 23:00)
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Jen malej tip. Lepší než si na začátku tupě napsat ty tři čísla, udělat mezi ně nějaké tečky a pak se pokoušet vzpomenout jestli se má násobit křížem vlevo nebo vpravo nebo podobné nesmysly, je počítat to mozkem. Nám to ve škole taky vysvětlovali takhle debilně, vždycky se to napsalo, prohlásilo se že je to přímá nebo nepřímá úměra, a pak se tam po stranách slavně nakreslily nějaké šipky, a podle nich se nějak šlo. Nevím už jak, ale byla to pitomost, a díky tomu jsem se to taky naučil až o dost později.
Např. ten příklad s kombajnem. Za 6,75 h pokosí 4,5 ha při rychlosti 6 km/h. Kolik tedy potřebuje času na 1 hektar? No přece 6,75/4,5=1,5 h. Když pojede šestkrát pomaleji, kolik času bude potřebovat na hektar? No přece šestkrát víc, když jede pomaleji. Takže při rychlosti 1 km/h potřebuje na 1 ha čas 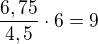 hodin.
hodin.
No jo, ale on teď pojede sedmkrát rychleji (takže to vydělím 7mi, protože mu to zabere kratší čas), ale bude chtít pokosit desetkrát tolik (takže to vynásobím deseti, protože čím víc toho má pokosit, tím déle to trvá). Celkem tedy potřebuje 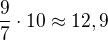 hodin.
hodin.
Takhle jdou řešit všechny ty úlohy. Jen se zamysli a spočítáš to. Slovo trojčlenka je smrt. Tím to pak zbytečně budí dojem, že je to nějaká raketová věda a je potřeba se to učit nazpamět.
Offline
#13 16. 10. 2013 23:11
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Ano pochopil :)
↑ LukasM:
Mě osobně to na ZŠ taky štvalo, ale naštěstí jsem si to vždycky řešila logicky a po svém. Vadí mi studenti, kteří jen dosazují do vzorců, vůbec o tom nepřemýšlí a učí se matiku stejně jako třeba Dějepis (nazpaměť). Bohužel je pravda, že většina studentů na to logicky nepřijde, pak jim nezbývá nic jiného než se to tak učit a nebo nosit pětky....
Offline
#14 16. 10. 2013 23:16
Re: Přímá a nepřímá úměrnost
↑ xstudentíkx:
Myslím, že většina studentů by na to logicky přišla. Akorát by jim někdo musel říct, že se o to mají snažit, a ne jim hned házet mechanické postupy a vzorce. Ale to sem až tolik nepatří.
Offline
#15 16. 10. 2013 23:18
Re: Přímá a nepřímá úměrnost
Ale např u toho příkladu č.3 to dosazuju stejně jako u ostatních, ale vychází to blbě..
6,75....6km/h....4,5ha
x...7km/h....10ha
Jinak já už jsem v prváku a ted jsme se k tomu najednou vrátili, takže netušim co a jak, Tím logickým způsobem bych to možná zvládl, ale je to pro mě zdlouhavé a zíra na to píšeme..
Offline
#16 16. 10. 2013 23:29
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ LukasM: Možná jo, ale spíš jsem se setkala s případy, kdy 2 hodiny vysvětluji logiku a stejně to nevyřeší, takže v poslední době, spíš volím vysvětlení mechanismu, jelikož na logiku, nemám trpělivost :)
↑ Mazarini:
Čísla pěkná nevyjdou, ale to je vina autorů, jinak postup je stejný (už jsem ho zde psala) :)
Alespoň vím, že nejsem na jediné střední, kde se opakuje, tak dlouho :)
Offline
#18 16. 10. 2013 23:39
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
xstudentíkx napsal(a):
↑ Mazarini:
a jelikož chceme zjistit jedno x, tak 405/31,5x=12,9.
To je zaokrouhlených 12,9.
Offline
#20 16. 10. 2013 23:52
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Je třeba si uvědomit co potřebuješ zjistit, tady v tom případě máš činnost, která něco vyprodukuje, takže mezi sebou budeme násobit činnosti a na druhé straně vykonanou práci.
6,75*6 (40,5).........4,5ha
x*7 (7x)................10ha
a teď 10*40,5=7x*4,5
a to je 405=31,5x
x= 12,9
Je třeba nad tím trochu přemýšlet a uvědomit si, co máš počítat a co znáš :)
Offline
#22 17. 10. 2013 00:01
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Přímá a nepřímá úměrnost
↑ Mazarini:
Rádo se stalo, hodně štěstí při testu :)
Offline
#23 17. 10. 2013 11:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přímá a nepřímá úměrnost
Zdravím v tématu, jen pár drobnosti:
a učí se matiku stejně jako třeba Dějepis (nazpaměť)
dějepis má také logiku, bohužel také se tak (obvykle) neučí.
Slovo trojčlenka je smrt. Tím to pak zbytečně budí dojem, že je to nějaká raketová věda a je potřeba se to učit nazpamět.
to jsi říkal i v týmu odpůrců trojčlenek. Ale opět - záleží, jak se učí. Pokud se vysvětlí podstata a šípky se používají jako pomůcky, tak žádný problém - zde jsem vysvětlovala o pomůckách (i s obrázkem) a zde o podstatě.
Ale nedoporučovala bych to tak hopem zavrhovat - je to historická součást počtů a do vývoje a do použití velmi dobře patří (že se pořádně nevysvětlí nebo nepochopí, to je něčem jiném).
Offline
#24 17. 10. 2013 16:10 — Editoval LukasM (17. 10. 2013 16:15)
Re: Přímá a nepřímá úměrnost
jelena napsal(a):
No jo, a to je už čtyři roky. To je jen vidět jak jsem dobrej, když mám názory pořád stejné. Politici by se ode mně mohli učit, těm to ty čtyři roky většinou nevydrží. Ale vážně. V tom vlákně jsme se na tom názoru v podstatě shodli, a každý s ním jistě souhlasí. Pomůcky jsou fajn, ale bohužel z některých se postupem času stávají postupy a návody. SŠ jsem prošel relativně nedávno a musím říct, že některé pomůcky by mi pomohly nejvíc, kdybych o nich nikdy nic neslyšel (resp. se o nich dozvěděl až s odstupem času). Ale to je asi jasné, na tom není co řešit:-)
Mimochodem, zrovna dneska jsem psal příspěvek ve kterém mj. také píšu, že vzorce jsou dobrý sluha a špatný pán.
Jinak tu diskuzi si ještě pamatuju, a tvůj odkaz mi připomněl že stárnu dost rychle. Co nejmíň takových, prosím :-)
Offline

 x
x 