Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Carmichael deli Eulera? (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 10. 2013 20:19 — Editoval M0M0 (19. 10. 2013 20:21)
Carmichael deli Eulera?
Zdravim, mal by som sa pokusit dokazat ze pan Charmichael bol sikovnejsi ako pan Euler a teda vysledky jeho funkcie delia Eulerove...prve dve pravidla funkcii su jasne ale neviem ako pokracovat..any hints?
Offline
- (téma jako vyřešené označil(a) M0M0)
#2 20. 10. 2013 03:59
Re: Carmichael deli Eulera?
↑ M0M0:
Carmichaelova funkcia priradí číslu n najmenšie kladné celé číslo m také, že 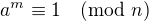 pre každé celé číslo a.
pre každé celé číslo a.
Ak  označíme najmenšie kladné celé s danou vlastnosťou, tak aj každé číslo tvaru
označíme najmenšie kladné celé s danou vlastnosťou, tak aj každé číslo tvaru  má takúto vlastnosť.
má takúto vlastnosť.
Navyše sa dá ukázať, že násobky  sú jediné čísla s takou vlastnosťou.
sú jediné čísla s takou vlastnosťou.
Ak totiž platí 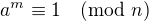 a m zapíšme (podľa vety o delení so zvyškom) ako
a m zapíšme (podľa vety o delení so zvyškom) ako 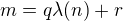 , tak máme
, tak máme 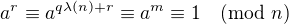 .
.
O zvyšku r vieme, že  . Ak by platilo
. Ak by platilo 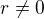 , tak by to bol spor s minimalitou čísla
, tak by to bol spor s minimalitou čísla  . (Číslo r je menšie ako
. (Číslo r je menšie ako  , a má danú vlastnosť.)
, a má danú vlastnosť.)
Offline
#5 20. 10. 2013 21:06
Re: Carmichael deli Eulera?
Poznamka:
Mozno aj toto ta bude zaujimat
http://en.wikipedia.org/wiki/Carmichael_number
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Carmichael deli Eulera? (TOTO TÉMA JE VYŘEŠENÉ)

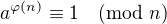 .
.