Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pravděpodobnost - nezávislost jevů (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 10. 2013 17:25 — Editoval Sulfan (25. 10. 2013 17:26)
Pravděpodobnost - nezávislost jevů
Dobrý den, řeším následující příklad z pravděpodobnosti:
Máme u schránek, v nichž je v každé m bílých a n černých stejně velkých obálek. Z prvé schránky náhodně vybereme obálku a vložíme ji do druhé. Z druhé opět vytáhneme jednu obálku a vložíme ji do třetí, atd. Určete pravděpodobnost toho, že po takovém přemístění vytáhneme z poslední schránky bílou obálku.
Uvažoval jsem od konce, pravděpodobnost, že v posledním tahu vytáhneme bílou obálku je rovna: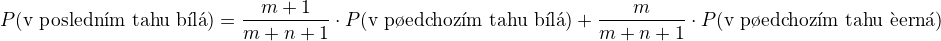
zároveň: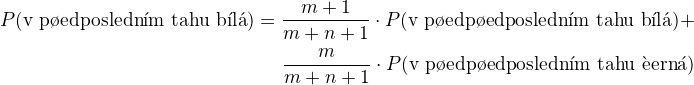
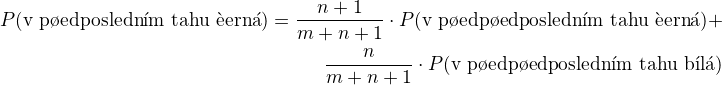
a nějakým způsobem rekurzivně dojít k prvnímu tahu a využít, že 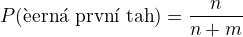
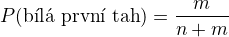
ale nevím jak. Věděl by někdo jak na to?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 25. 10. 2013 22:46 — Editoval Jj (25. 10. 2013 22:51)
Re: Pravděpodobnost - nezávislost jevů
↑ Sulfan:
Pb,i - pravděpodobnost tahu bílé v i-tém tahu
Pc,i - detto černé
m + n = p
Řekl bych, že pro tah č. i+1 (kromě prvního) bude v souladu s Vámi uvedenými vztahy platit: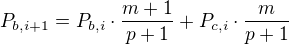
Pro libovolný tah musí platit: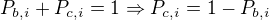
Čili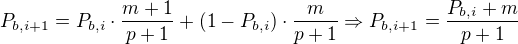
a s využitím počáteční podmínky 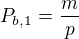 po úpravách obdržíme:
po úpravách obdržíme: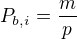 pro i = 1,2,3, ... u
pro i = 1,2,3, ... u
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pravděpodobnost - nezávislost jevů (TOTO TÉMA JE VYŘEŠENÉ)
