Matematické Fórum

petulkacip · 04. 02. 2009 20:12

ahojky,
nejak nemuzu prijit na postup, mohli byste mi to prosim polopate vysvetlit?

je dana funkce f(x): y=-2+log2(x-1). urcete interval na nemz existuje k funkci f(x) fce inverzni. vyjadrete inverzni funkce f na minius prvni(y) a f na minus prvni (x), urcete D(f na minus prvni (x) a obor H(f) na minus prvni(x) nacrtni graf funkce f na minus prvni (x) a urci souradnice pruseciku grafu se souradnicovymi osami...

a to same zadani pro f(x) y=-2+3 na x-1

dekuji moc moc!!!

vosa · 04. 02. 2009 20:48 — Editoval vosa (04. 02. 2009 20:50)

interval na kterém k funkci existuje funkce inverzní, je takový, na kterém je funkce prostá. Což u této funkce, pokud dobře vidím, je celý Df.
Takže nejdřív určit Df: musí platit x-1 > 0, takže Df = (1, nekonecno)

vyjádření inverzní funkce:
$y = -2+\log_2{(x-1)} \nl y+2=\log_2{(x-1)} \nl 2^{y+2} = x-1 \nl 2^{y+2} +1=x$

Takže: $f^{-1}(x) = 2^{x+2} +1 \quad \forall x \in R$
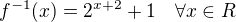
obor hodnot je ta část def. oboru f, na které byla f prostá, tj v tomto případě celý Df: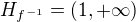
$H_{f^{-1}} = (1, + \infty)$
Průsečíky: graf se s osou y protíná v bodě x = 0, čili 2^(0+2) +1 = 5 = y
s osou x se graf neprotíná, jak je vidět z oboru hodnot, (v průsečíku by funkce musela nabývat hodnoty 0)

Grafem je exponenciela (o základu 2, pokud jsem správně pochopila zadání :) posunutá o 1 nahoru a o 2 do leva.

petulkacip · 04. 02. 2009 22:46

↑ vosa:
moc dekuju:)

Matematické Fórum

#1 04. 02. 2009 20:12

inverzni funkce

#2 04. 02. 2009 20:48 — Editoval vosa (04. 02. 2009 20:50)

Re: inverzni funkce

#3 04. 02. 2009 22:46

Re: inverzni funkce

Zápatí