Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 26. 11. 2013 09:56
Re: Limita
↑ Mirgeee:
Ahoj,
ano, sečíst to neumíme, takže asi bude třeba sevřít. Spodní odhad je jednoduchý: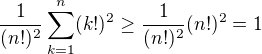 .
.
Ten horní je horší, ale dá se taky ukázat, že to je jednička. Klíčový (ale jednoduchý) trik je napsat si to takhle: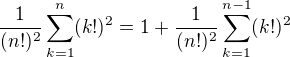 .
.
Teď je třeba odhadnout tu poslední sumu shora výrazem, který jde k nule, což už není těžké. Pro kontrolu:
Můžeš si pak snadno ověřit, že bez toho triku by tento poslední odhad nefungoval.
Offline
#3 27. 11. 2013 01:26
Re: Limita
Ahoj,
pěkný odhad, toto by také mohlo fungovat http://cs.wikipedia.org/wiki/Stolzova_v%C4%9Bta .
Offline
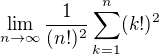

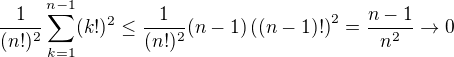 .
.