Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 12. 2013 19:47
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Nevlastní integrál - co je špatně?
primitivni funkce je dobre, dal se to neda precist.
Offline
#3 02. 12. 2013 19:54 — Editoval kaja.marik (02. 12. 2013 19:55)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Nevlastní integrál - co je špatně?
Fijojo napsal(a):
...Popř. umí MAW ...
Ne, MAW ne, zkuste http://sagecell.sagemath.org/ a zadat
Code:
show(integrate(1/(x^2+3),x,-infinity,0))
Offline
#4 02. 12. 2013 20:03
Re: Nevlastní integrál - co je špatně?
↑ kaja.marik:
Má to být 0 mínus (mínus nekonečno) a je jasné, že to je blbě asi, že to se výsledku ani trochu nepodobá.
Offline
#6 02. 12. 2013 20:55
Re: Nevlastní integrál - co je špatně?
↑ Brzls:![kopírovat do textarea $\int_{-\infty }^{0}\frac{1}{x^2+3}dx=\lim_{a\to-\infty }\int_{a }^{0}\frac{1}{x^2+3}dx=\lim_{a\to-\infty }[\frac{1}{\sqrt{3}}arctg\frac{x}{\sqrt{3}}]=$](/mathtex/59/59a3b404ba9dc21360a1fad6e7043b4d.gif)
Vzorec: V11 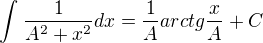
do výrazu doplním 0=> dostanu 0
mínus
do výrazu doplním a ( )
)
=  ??
??
Spočítal jsem předtím 5 příkladů a neměl jsem problém, tak nechápu, proč zrovna u tohoto jsem to spočítal špatně...díky...
Offline
#7 02. 12. 2013 20:59 — Editoval Fijojo (02. 12. 2013 20:59)
Re: Nevlastní integrál - co je špatně?
↑ kaja.marik:
Program to spočítá pěkně :)), škoda jen, že je to bez postupu...
Offline
#8 02. 12. 2013 21:04 — Editoval Brzls (02. 12. 2013 21:05)
Re: Nevlastní integrál - co je špatně?
Tak si ten graf funkce arkus tangens představ. Když do funkce tangens dosadíš nějaké číslo málo se lišící od mínus pí/2 tak dostaneš nějaké obrovské záporné číslo (to je snad jansý). Lze tedy očekávat, že když do invezní funkce dosadíš nějaké obrovské záporné číslo, tak dostaneš něco blízké mínus pí/2
Tady je ten graf
http://cs.wikipedia.org/wiki/Soubor:Arctg.png
Offline