Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2014 07:26
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Lagragián soustavy
Zdravím,
potřeboval bych pomoc s timto příkladem - mám zde soustavu s tuhou tyčkou o hmotnosti m a o celkové délce l, kde jeden konec tyčky se nachází na svislé ose y a druhý konec se nachází na vodorovné ose x. Střed této tyčky je připojen k počátku souřadnicového systému pomocí pružinky o tuhosti k. Jak vypadaá lagrangián soustavy?
Lagrangián vypočítam s pomocí Lagrangeovy funkce  . Byl bych moc vděčný kdybyste mi napsali jak mají vypadat ty energie
. Byl bych moc vděčný kdybyste mi napsali jak mají vypadat ty energie  (kinetická energie soustavy) a
(kinetická energie soustavy) a  (potencialní energie soustavy). Vubec si nevím rady s tím co vše by se do těch energíí mělo zahrnout. Děkuju
(potencialní energie soustavy). Vubec si nevím rady s tím co vše by se do těch energíí mělo zahrnout. Děkuju
Offline
- (téma jako vyřešené označil(a) OndraVesely)
#2 19. 01. 2014 10:29
Re: Lagragián soustavy
Vubec si nevím rady s tím co vše by se do těch energíí mělo zahrnout.
potenciální energie pružiny
potenciální energie těžiště tyče
kinetická energie posuvného pohybu tyče
kinetická energie otáčivého pohybu tyče kolem těžiště
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 19. 01. 2014 11:27
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Re: Lagragián soustavy
↑ zdenek1:
Děkuju, přesně to jsem chtěl vědět, je toto v pořádku?
kinetická energie otáčivého pohybu tyče kolem těžiště 
kinetická energie posuvného pohybu tyče=
potenciální energie pružiny 
potenciální energie těžiště tyče 
Offline
#4 19. 01. 2014 11:46
Re: Lagragián soustavy
↑ OndraVesely:
Ano, ale pro výpočet to bude chtít vyjádřit proměnné ( ,
,  ,
,  ,
,  ) pomocí jednoho parametru. Já osobně bych si vybral úhel OAB
) pomocí jednoho parametru. Já osobně bych si vybral úhel OAB
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 19. 01. 2014 11:49 — Editoval OndraVesely (19. 01. 2014 15:54)
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Re: Lagragián soustavy
jj, díky moc
Je toto v pořádku? Nejsem si jistý tou úhlovou rychlostí  .
.  , kde úhel
, kde úhel 





Offline
#6 19. 01. 2014 16:54
Re: Lagragián soustavy
↑ OndraVesely:
ty derivace  ,
,  nejsou dobře,
nejsou dobře,  je konstanta
je konstanta
a také 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 19. 01. 2014 17:52
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Re: Lagragián soustavy
↑ zdenek1:No jo, to jsem ale popleta
Mužete mi ještě prosím zkontrolovat zdali je tento postup správný:
1. 



2. Dosadim vše do rovnice 
3. Dosadím do Lagrangiánu  - kde za
- kde za 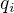 dosazuji postupně
dosazuji postupně 
Offline
#8 19. 01. 2014 18:05
Re: Lagragián soustavy
↑ OndraVesely: proč "mínus"?
proč "mínus"?
3. proměnné vyjadřuješ pomocí jednoho parametru právě proto, abys za 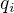 už dosazoval jen ten parametr, tj.
už dosazoval jen ten parametr, tj. 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 19. 01. 2014 18:11
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Re: Lagragián soustavy
↑ zdenek1:lol, díky moc
Offline