Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Korelace tří veličin (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 01. 2014 14:39
Korelace tří veličin
Ahoj,
dostal jsem se k následujícímu problému a nějak mi to po pondělku nemyslí. Mohl by mě někdo, prosím, nakopnout do správného směru úvah?
Problém: Mám tři veličiny E1, E2 a D, prakticky jsou E1 a E2 řadou zjednodušení zatížené odhady teoretické hodnoty D. Podle publikovaných výsledků bývá Pearsonův korelační koeficient mezi E1 a D i mezi E2 a D v nejhorším případě 0.8. Můžu pouze na základě této znalosti učinit nějaký smysluplný odhad nejhoršího možného korelačního koeficientu mezi E1 a E2?
Доктор сказал «в морг» — значит в морг!
Offline
- (téma jako vyřešené označil(a) Formol)
#2 20. 01. 2014 15:18
Re: Korelace tří veličin
Uz som tu take podobne riesil
http://forum.matweb.cz/viewtopic.php?id=50398
prispevok #4
Offline
#4 20. 01. 2014 15:39
Re: Korelace tří veličin
bohuzial ak pouzijes ten vzorec co mi tam vysiel, tak len z toho co si zadal nevies povedat nic, lebo ak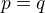 tak moze nadobudat cokolvek z
tak moze nadobudat cokolvek z ![kopírovat do textarea $[2p^2-1,1]$](/mathtex/57/578bd6fa5a60e8db95c44553e48b6309.gif) a ak
a ak tak moze nadobudat cokolvek z
tak moze nadobudat cokolvek z ![kopírovat do textarea $[-1,1-2p^2]$](/mathtex/43/43f41153d6da9c87ba2f1f0e1562c8ab.gif)
teda ak ![kopírovat do textarea $p,q\in [-k,k]$](/mathtex/00/002f562be198b7b1c58f6eeaf609fca7.gif) tak vysledny koeficient je cokolvek z
tak vysledny koeficient je cokolvek z ![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) - teda cokolvek
- teda cokolvek
Offline
#5 20. 01. 2014 17:09
Re: Korelace tří veličin
↑ Brano:
Děkuji za upozornění, špatně jsem se vyjádřil, tohle pro mě je "jen" kontrola smysluplnosti výsledků. Korelační koeficient E1 a E2 mi vyšel poměrně nízký a tak jsem se obával, že to signalizuje chybu. Díky tvému postupu ale vím, že mám stále v principu možný výsledek. Dokonce je to jistým způsobem vítaný výsledek, ale to už by bylo zabíhání do detailů, které nejsou moc matematické (není to tajné, takže pokud by tě to zajímalo, můžu se rozepsat).
Доктор сказал «в морг» — значит в морг!
Offline
#6 20. 01. 2014 17:18
Re: Korelace tří veličin
↑ Formol:
mna statisticke analyzy nejak extra nebavia, takze nemusis pisat kde to vzniklo.
ja som ten druhy prispevok zacal pisat este predtym ako som si vsimol tvoju odpoved, ze to uz bolo dostatocne
a vyzera ze som asi aj tak zle interpretoval "v nahorsom pripade 0.8" lebo to asi znamenalo![kopírovat do textarea $p,q\in [0.8,1]$](/mathtex/1e/1efcf9f18138d89f559e7d1bae2d877f.gif) a nie
a nie ![kopírovat do textarea $p,q\in [-0.8,0.8]$](/mathtex/7f/7f8b17633ced46e9c86e3a5326dbaf30.gif) ze?
ze?
Offline
#7 20. 01. 2014 17:40
Re: Korelace tří veličin
↑ Brano:
Ano, oba korelační koeficienty jsou kladné. Tím v nejhorším případě jsem myslel tak, že bylo publikováno několik měření a korelační koeficient nevyšel nikdy menší než 0.8.
Доктор сказал «в морг» — значит в морг!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Korelace tří veličin (TOTO TÉMA JE VYŘEŠENÉ)
